期刊: Mechanical Systems and Signal Processing(IF:8.4)
创新点
- 本文提出了一种新型故障诊断方法,可同时处理不同类型的数据。该模型结合了用于数值输入的 MLP 和用于 HHT 图像的 CNN。
- 本文提供了一个新的数据集,该数据集是通过直接安装在转轴上的 WAS 获得的。该数据集在本文第 3 节中进行了描述,可在公共领域获取。我们鼓励其他研究人员开发适用于这一独特数据集的增强型诊断方法。
相关工作
线性信号到图像转换
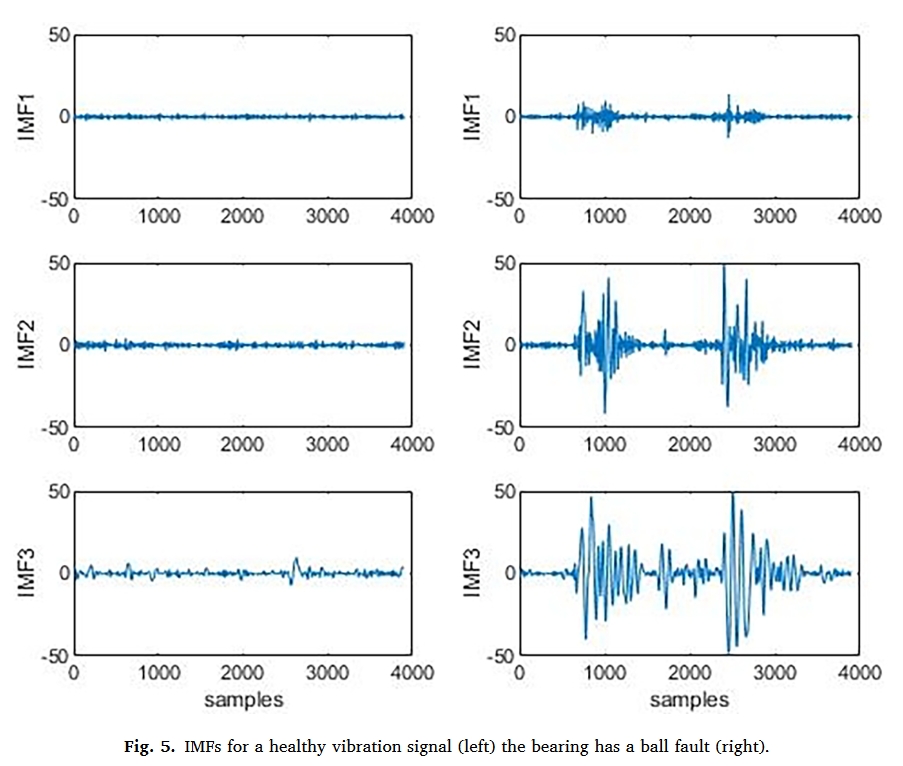
希尔伯特-黄变换是经验模式分解(EMD)和希尔伯特变换的结合,是一种针对非线性和非稳态数据的时频分析方法。它常用于分析具有复杂频率成分的轴承信号。
利用 EMD,可将任意信号自适应分解为一系列本征模式函数(IMF),并可表示为 IMF 的总和加上一个残差项:
$x(t)=\sum_kIMF_k(t)+r(t)$
EMD 之后,希尔伯特变换可分别应用于每个 IMF。任何信号 x(t) 的希尔伯特变换 y(t) 定义为:
$y(t)=\frac1\pi\int_{-\infty}^\infty x(t)/(t-\tau)d\tau $
利用 y(t) 和 x(t),相关分析信号 z(t) 的定义为:
$z(t)=x(t)+iy(t)=a(t)e^{i\theta(t)}$
其中,a(t) 是信号的包络线,θ(t) 是瞬时相位。瞬时频率可以通过瞬时相位的导数计算出来:
$\omega(t)=\frac d{dt}\theta(t)$
对每个 IMF 进行希尔伯特变换后,原始信号的实部(R)可以用下面的形式表示。
$x(t)=\Re\left(\sum_ja_j(t)e^{i\theta_j(t)}\right)=\Re\left(\sum_ja_j(t)e^{i\int\omega_j(t)dt}\right)$
上式给出了每个分量的振幅和频率与时间的函数关系。这种振幅的时频分布称为希尔伯特频谱。
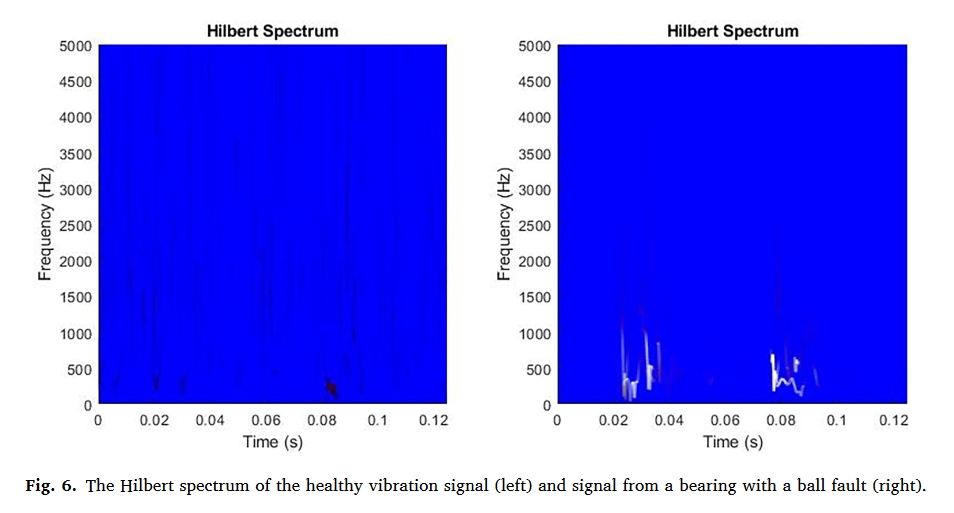
图 5 描述了有故障和无故障轴承线性信号的分解过程。只建立了前三个固有模态函数。可以看出,不同类型信号的本征模态函数差别很大。图 6 描述了前三个本征模态函数对应的 HHT 频谱。
在传统的 HHT 方法中,整个信号的希尔伯特频谱是通过转换所有获得的 EMD 分解结果得到的。不过,仅使用前几个 IMF 生成希尔伯特频谱也能获得较好的结果,并降低了计算成本[37,38]。我们的大量实验表明,只使用前三个 IMF 是最有效的。
角度信号到数字的转换
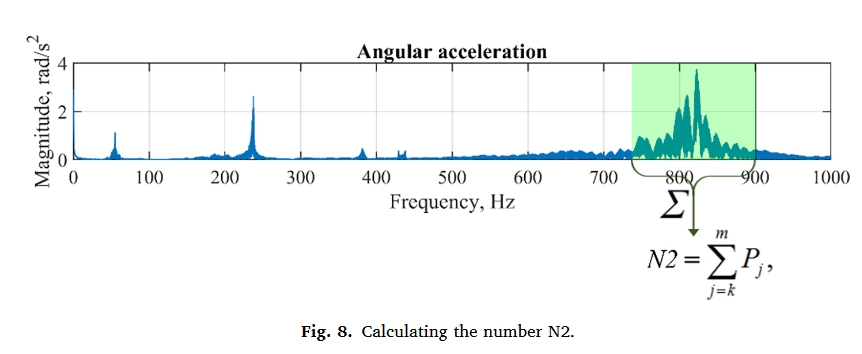
N1 和 N2 值基于缺陷行为的脉冲模型。轴承中的每个缺陷都会产生冲击,从而激发自然机械频率。周期性冲击会在固有频率周围产生调制频率成分,包括扭转模式(角加速度频谱)。随着时间的推移,轴承缺陷的增加会导致现有频率成分的增强和新频率成分的出现。
因此,分析固有频率周围的角加速度信号功率有助于轴承故障检测。在这里,扭转固有频率是通过冲击响应谱(SRS)分析找到的。SRS 分析包含三个步骤:
(1) 使用锤子对轴产生冲击。固定在轴上的 WAS 传感器测量冲击响应。
(2) 根据传感器响应的数学模型,将原始信号分解为角加速度和线性加速度。
(3) 通过 FFT 分析找到角加速度频谱的频率峰值。由此得到的频率峰值就是信号功率估计带的中心。
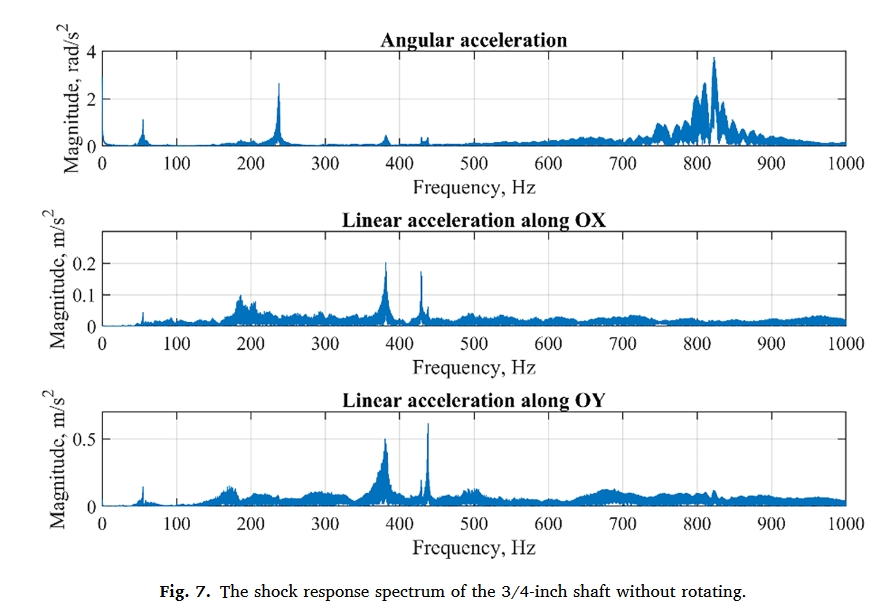
图 7 显示了本工作中使用的 3/4 英寸轴的 SRS,每个轴(角加速度和 X-Y 线速度)都有数据。
角加速度 SRS 在大约 240 Hz 和 820 Hz 处有两个明显的峰值,分别对应于 3/4 英寸轴的第一和第二扭转自然频率。N1 和 N2 的值是根据第一和第二个频率峰值周围的 FFT 分量之和计算得出的(图 8)。数值 N1 和 N2 与轴承缺陷有关。
方法
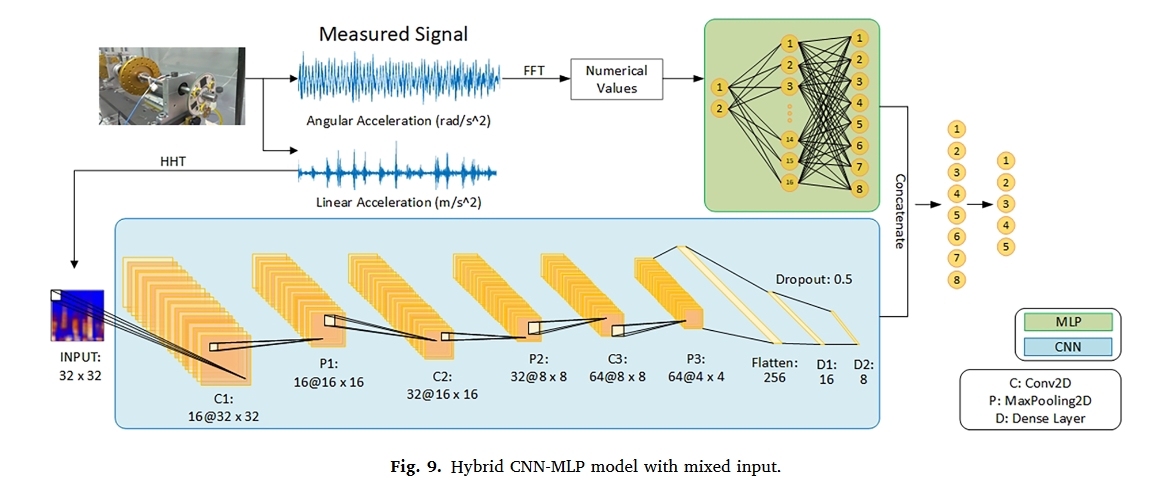
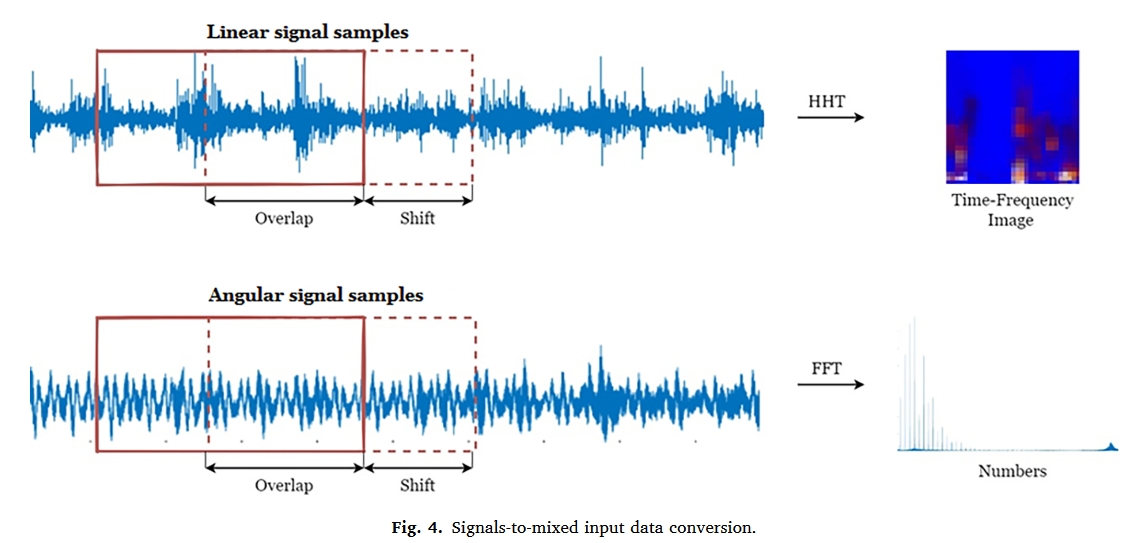
实验
数据集
自建
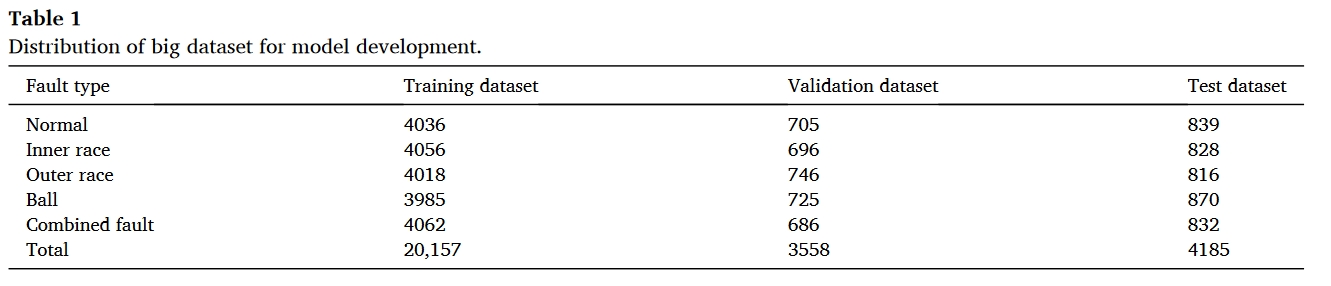
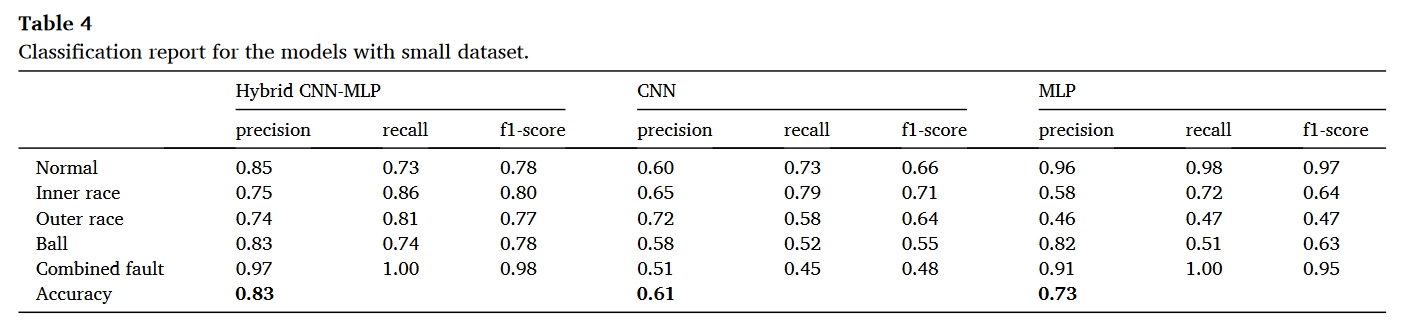
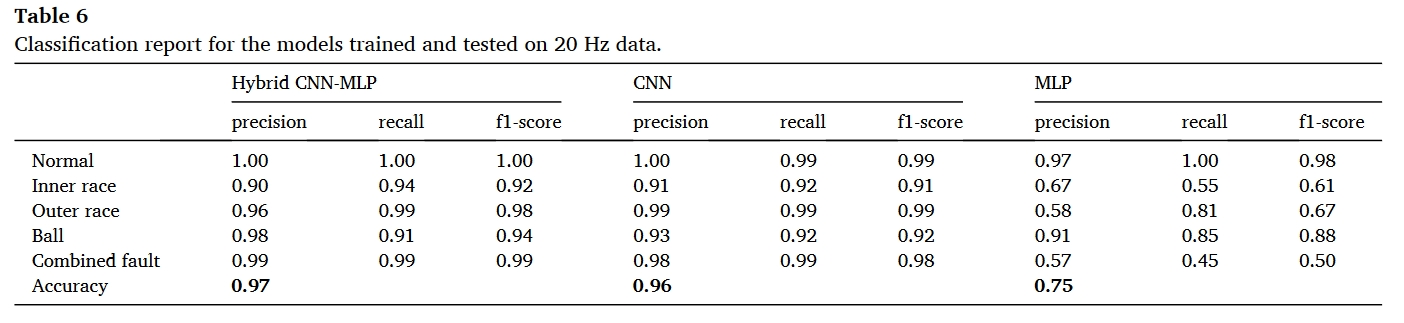
实际上,为每个故障案例收集大量数据集是一项挑战。此外,工业中的许多技术过程(如冶金和机械工程)都具有周期性和非稳定性特征。因此,混合模型的检测和定位效率是在接近现实的条件下,通过小数据集(转速为 20 Hz)进行训练估算出来的。此外,还估算了使用 18 赫兹转速数据集进行测试的混合模型的检测和定位效率。小数据集(转速为 20 赫兹)有 1382/245/288 个样本用于训练/验证/测试,而大数据集有 20157/3558/4185 个样本。表 4 提供了三种模型的分类报告。可以看出,与表 3 中的准确率相比,所有模型的准确率都大幅下降。这是因为小数据集的训练数据少了 14 倍。
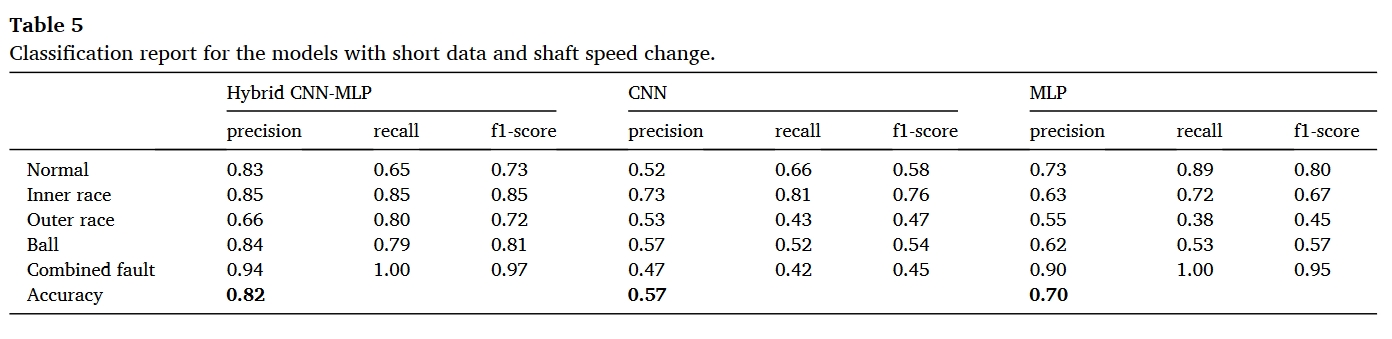
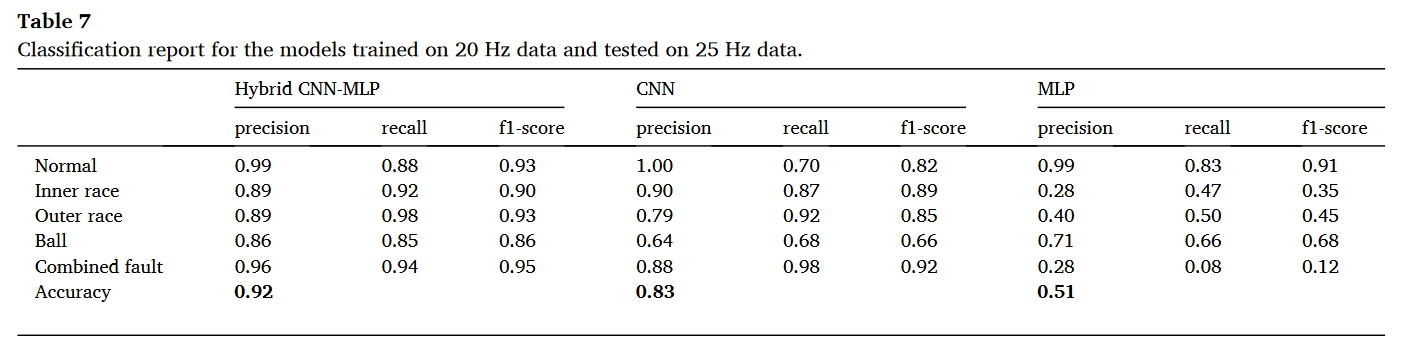
在本节中,我们将以轴转速从 20 Hz 变为 25 Hz 为例进行分析。HybridCNN-MLP 模型必须在具有挑战性的条件下工作–它将在 20 Hz 轴速下获得的数据上进行训练,并在 25 Hz 轴速下的数据上进行测试。与 20 赫兹相比,在 25 赫兹的情况下,故障更容易激发高频共振,从而提高传统方法的检测精度。因此,将混合 CNN-MLP 模型的性能与传统方法的效率进行比较是很有意义的。此外,还将比较每种方法处理信号和判断轴承状况所花费的时间。
对比方法
- CNN
- MLP
结果
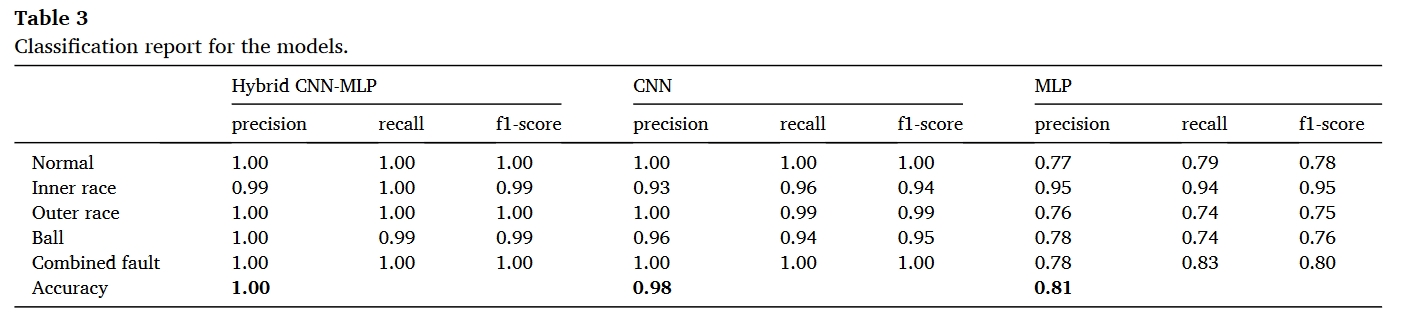
总结
- 提供了一种新的一维转二维的方法:Hilbert–Huang transform (HHT)。结合之前的小波变换、FFT、直接转换,现在有有多种方法进行转换。
- 提供了一种新的数据收集思路,即直接安装震动信号收集器在转子部件上,收集其角速度信息,然后通过FFT提取频域信息。