期刊: Measurement(IF:5.6)
创新点
本文提出了一种基于傅立叶变换和递推图(FT-RP)的数据处理方法。时间序列变换产生的二维数据被用作输入特征数据。
结合残差网络和注意机制等的骨干网络对 MAML 进行了改进。大边际高斯混合(L-GM)损失函数取代了完全连接层作为分类器,从而提高了 MAML 的跨域诊断性能。
方法
Model Agnostic Meta-Learning(模型无关元学习)
模型无关元学习(MAML)[28] 是一种基于优化的元学习方法。MAML 可以提供用于训练基础学习器的元学习器,其中元学习器是 MAML 中用于学习的主要部分,而基础学习器是在数据集上训练并用于测试任务的部分。大多数深度学习模型都可以作为基础学习器嵌入到 MAML 中。与模型无关并不意味着可以使用任何模型;相反,它意味着可以使用任何可以通过梯度下降进行优化和训练的模型。MAML 用途广泛,可用于分类、回归和强化学习。
MAML 的关键在于训练一组初始化参数,并通过在初始参数基础上应用一个或多个梯度更新步骤,利用有限的数据量快速适应新任务。该模型使用 N 向 K-shot 任务(训练任务)进行元学习训练,以确保获得 “先验知识”(初始化参数)。此外,这些 “先验知识 “还能提高新的 N 路 K-shot 任务的性能。在 MAML 训练过程中,优化分为两个循环:内环是训练程序,用于开发执行该任务的基本能力,而外环是元训练程序,用于开发跨任务的泛化能力。
训练数据和测试数据分别设置为 D tr 和 D test。用于训练的基础学习模型为 Mmeta,Mmeta 的初始化参数为 φ;用于 D 测试分类的模型为 Mtest。Mmeta 和 Mtest 的模型结构相同,只是参数不同。MAML 算法的流程为:
- 任务的支持集用于训练 Mmeta,并在此进行第一次梯度下降。(假设每个任务只有一次梯度下降)。
- 上一步用于在 N 个任务中训练 Mmeta,然后使用 N 个任务中的查询集来测试参数为 θ ̂i(i∈[ 1,N])的 Mmeta 的性能,从而得到总损失函数 L。
- 得到总损失函数后,进行第二次梯度下降。即更新初始化参数φ。
- 根据该初始化参数 φ 和模型 Mmeta,利用数据集 Dtest测试的支持集对该模型进行微调。
- 微调后,使用 Dtest测试的查询集对该模型进行评估。
提出的FT-PR预处理
滚动轴承的原始故障振动信号是一个时间序列。在滚动轴承的少量故障诊断问题中,每个工况只有少量训练样本,这意味着需要经过一定的处理才能提取振动信号中包含的特征信息。此外,在跨域故障诊断场景中,对域变化不敏感的特征数据更有利于成功诊断。为了获得对域不敏感的特征丰富的训练数据,本文提出了一种结合傅立叶变换和递推图的 FT-RP 数据预处理方法。
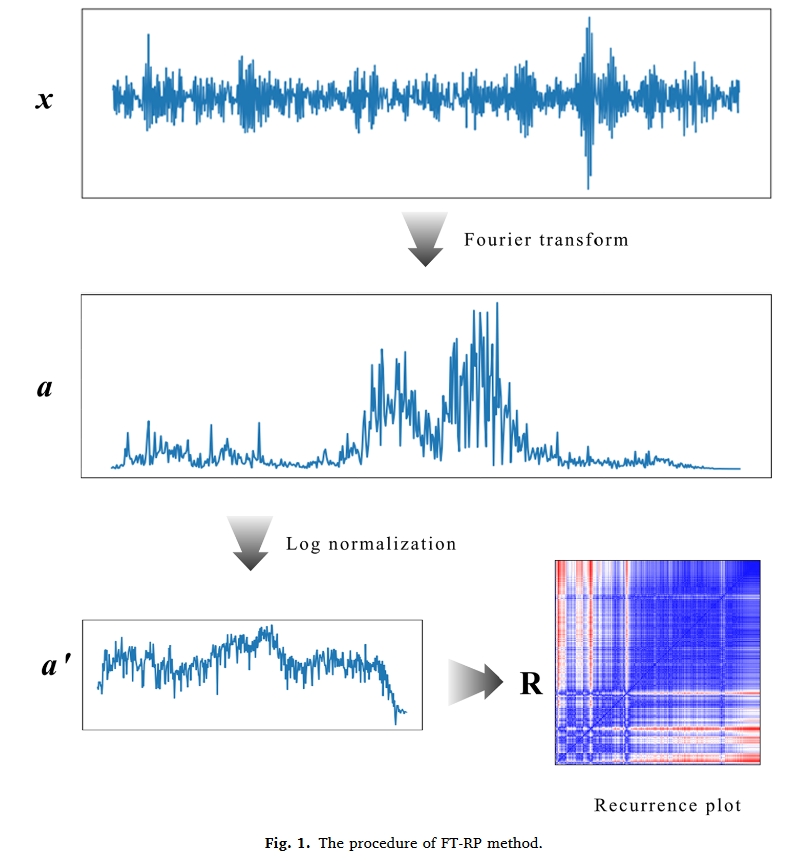
傅立叶变换可以提取振动信号的频域特征。递推图可以直观地将机械振动信号在高维相空间中的运动状态映射到二维平面上,从而直接定义和可视化其动态行为。实验表明,当频域信号转换为递推图时,会比直接使用时域信号表现出更明显的特征。
FT-RP 方法如图 1 所示。假设一段轴承振动信号为 x =[ x1, x2, ⋯, xL],首先用 Zscore 对其进行归一化处理,然后利用傅里叶变换得到信号单边谱的幅值 a。
$a=\mathscr{F}\left[\frac{x-\mu}\sigma\right]=[y_1,y_2,\cdots,y_n],n=L/2$
$a^{́}=\frac{\log(a+1)}{\log(\max(a+1))}=[{y}_1,{y}_2,\cdots,{y}_n]\in[0,1]$
对 a 进行对数归一化处理,以调整数据的分布,使其位于区间 [0, 1] 内。最后,生成 a ′ 的递推图 R。
$$R=RP(a^{^{\prime}})=\begin{bmatrix}z_{1,1}&z_{1,2}&\cdots&z_{1,n}\z_{2,1}&z_{2,2}&\cdots&z_{2,n}\\vdots&\vdots&\ddots&\vdots\z_{n,1}&z_{n,2}&\cdots&z_{n,n}\end{bmatrix}$$
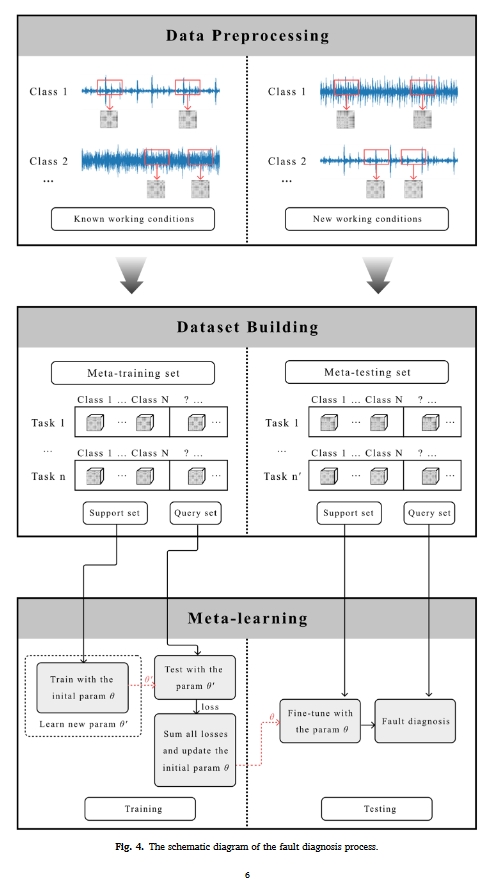
结构
实验
数据集
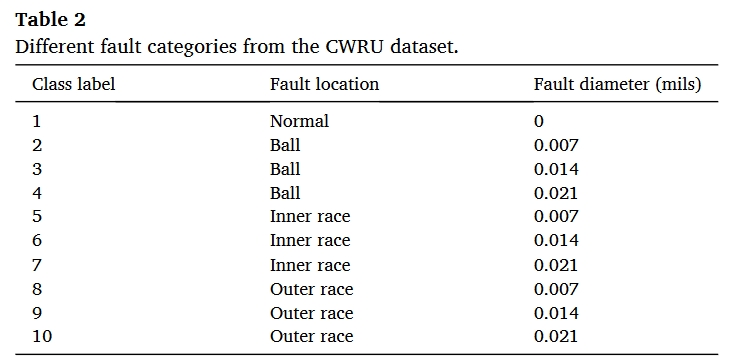
- CWRU
- Gear(自建)
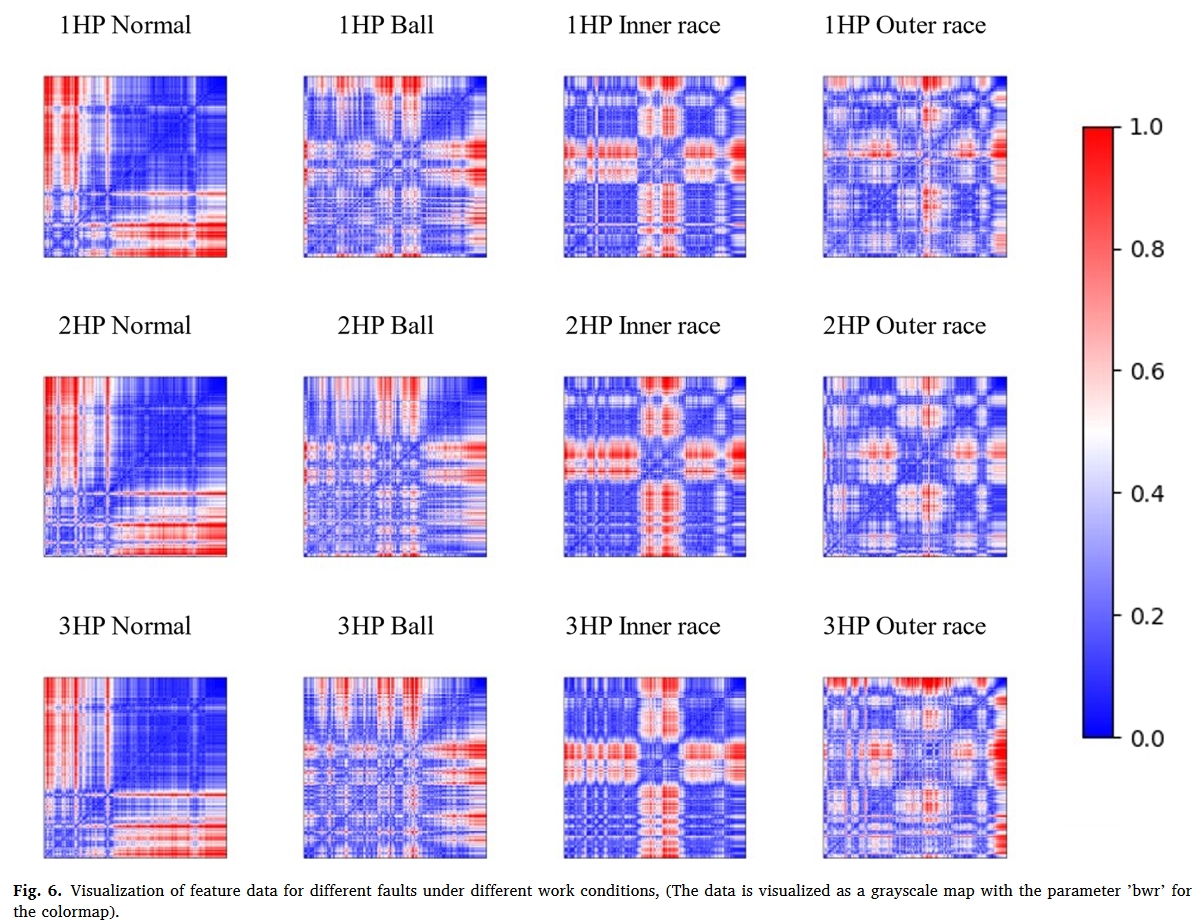
对比方法
- Siamese network-2020-Sensors
- relation network-2020-Measurement
- Prototypical network-2020-ICEIEC
- original MAML
结果
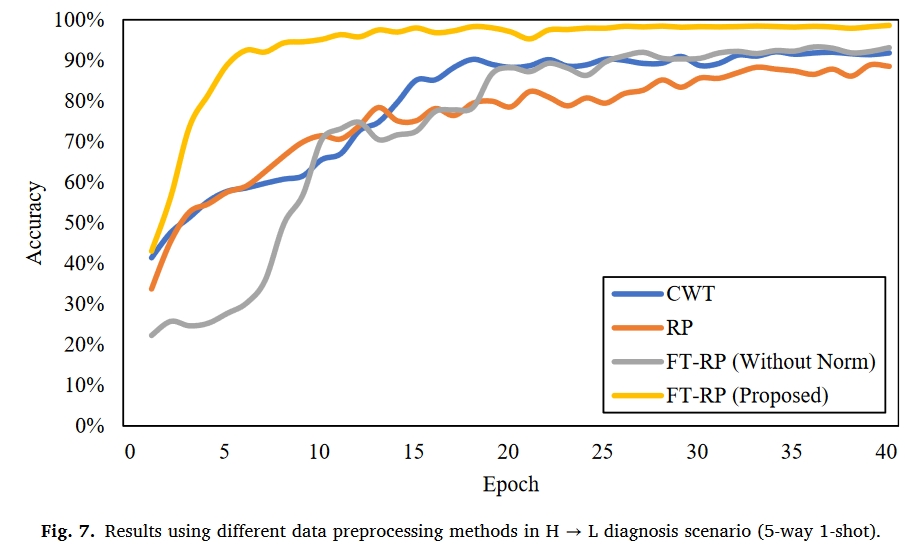
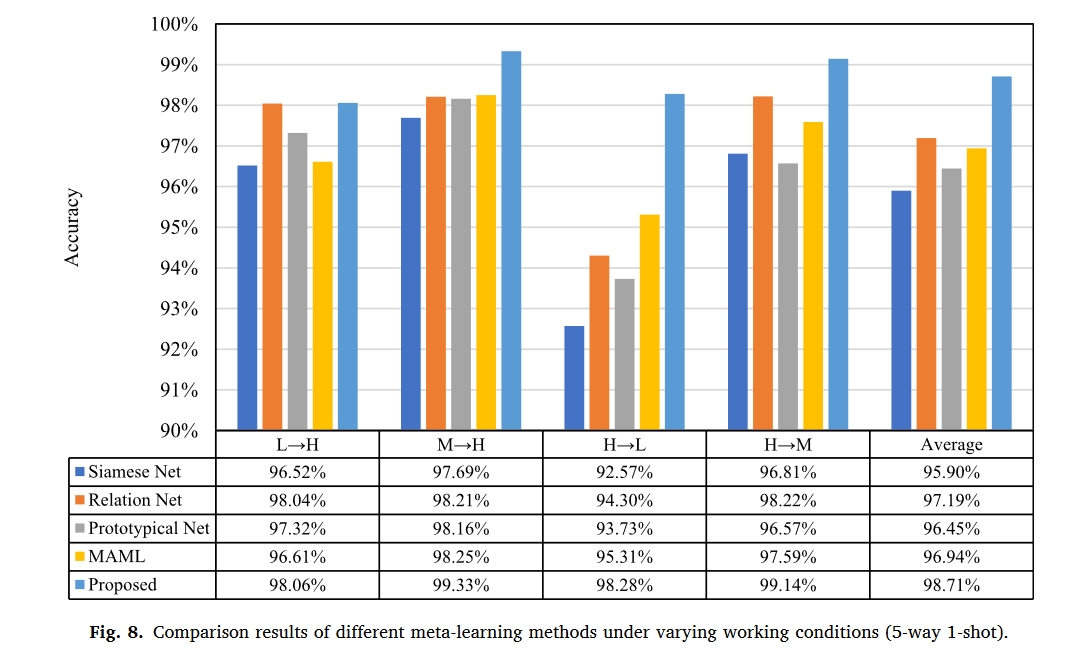

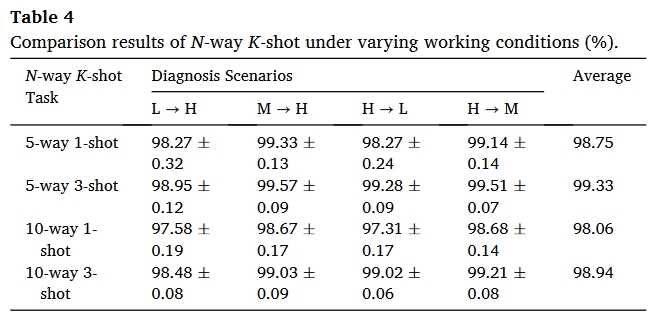
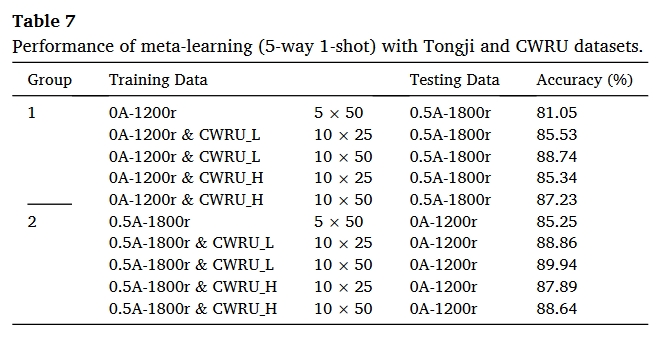
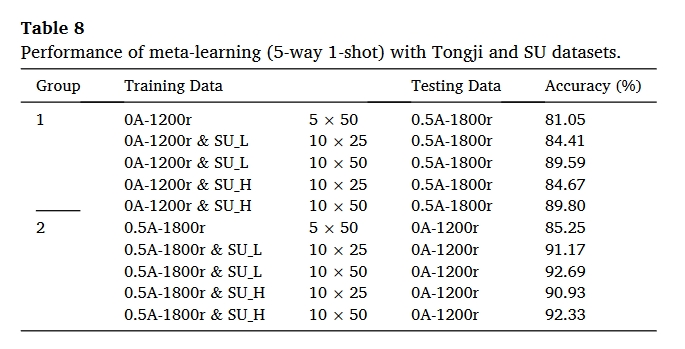
总结
又提供了一种一维信号转二维的方法:FT-PR;以及模型无关元学习的方案。