期刊: Knowledge-Based Systems(IF:8.8)
创新点
- 设计了一种标签分配策略(LAS),以充分利用未标记样本的信息,并有效抑制 OOD 样本的干扰。
- 定义了一个可扩展的距离度量函数,以灵活描述故障样本之间的相似性,并有效提取整个诊断任务空间的通用特征。
相关技术
元学习
元学习遵循情景学习范式,旨在利用先前的知识和经验指导新任务的学习,使网络能够学习。元学习训练的内环被称为episode,而外环是epoch。内环训练包含许多元任务,每个单独的元任务是元学习分类的基本单元。
每个元任务由两个子集组成:一个支持集S和一个查询集Q。对于每个元任务,假设支持集$S={(x
^s_1,y^s_1),…,(x^s_i,y^s_i),…(x^s_{N×K},y^s_{N×K})}$,其中xs i表示支持集中的第i个样本,标签为ys i,N表示支持集中包含的类的数量,K表示每个类的样本数量;查询集$Q={(xq1,yq1),…,(x^q_i,y^q_i),…(x^q_{N×L},y^q_{N×L})}$,其中$x_{qi}$表示查询集中的第i个样本,$y^q_i$表示与$x^q_i$对应的标签,L表示查询集中每个类的样本数。这个元学习分类问题被称为“N向K镜头”。在元学习中,每个元任务的训练样本总数为K+L,通常不大于20。
基于度量的元学习
原型网络(ProNet) 是一种经典的基于度量的元学习模型。其主要思想是利用距离度量学习两个样本之间的相似性,然后利用特征提取器将它们映射到不同的类别中。在解决新任务时,它可以很好地利用从以前任务中学到的元知识。
从原始数据集中随机抽取一些样本作为支持集和查询集,用于每个元任务的训练。支持集的每一类样本通过特征提取器 $f_\phi( \cdot)$ 生成特征向量,其中包含可学习参数 φ:
$C_k=\frac1{|S_k|}\sum_{(x_i^s,y_i^s)\in S_k}f_{\varphi}(x_i^s),$
其中,$C_k$ 是类别 $k$ 的原型,$S_k$ 代表类别 $k$ 中样本的总数量,$x^s_i$ 是属于类别 $k$ 的样本,$y^s_i$ 是 $x^s_i$ 的标签。
每个任务下的查询集样本用于训练和更新特征提取器的参数 φ。通过测量样本与所有原型之间的距离来确定最接近的原型,从而完成对样本的分类。查询集样本属于类别 k 的预测概率计算如下:
$P_{\varphi}(y=k\left|x\right)=\frac{\exp\left[-d\left{f_{\varphi}(x_{i}^{q}),C_{k}\right}\right]}{\sum_{u}\exp\left[-d\left{f_{\varphi}(x_{i}^{q}),C_{u}\right}\right]},$
其中 d {a, b} 表示 a 和 b 之间的度量距离。
方法
Label allocation strategy design (LAS)
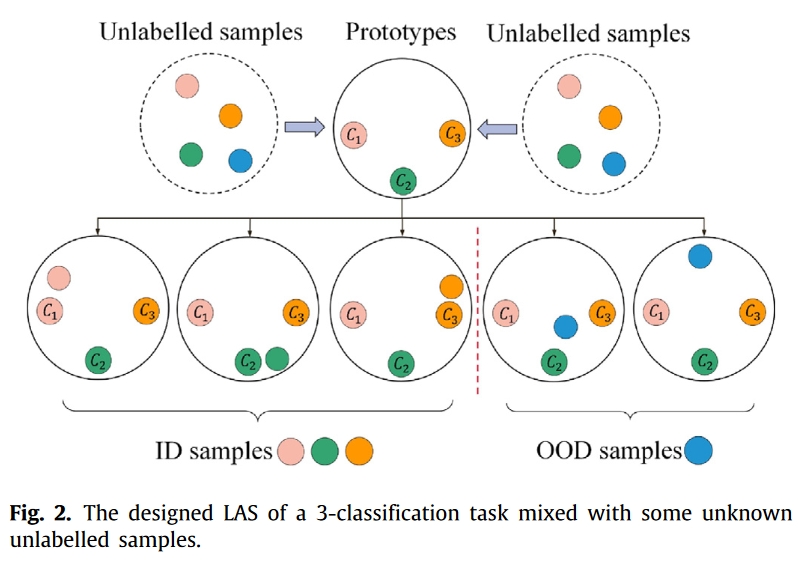
虽然半监督学习(SSL)算法有望解决少数标记样本下的模型过拟合问题,但当非标记样本中包含一些 OOD 样本时,其性能可能会受到严重影响。基于此,本研究设计了一种 LAS,既能充分利用隐藏在未标记样本中的有用信息,又能抑制未知 OOD 样本的干扰。具体步骤如下:
计算每个类别的原型:对于’’N-way K-shot’’元任务中每个类别的标记样本,公式(1)用于生成每个类别的原型。原型集表示为 $C = {Ck}^N_{k=1}$ 。
定义距离矩阵:对于每个未标记的样本 xu i,其空间特征向量$ f_φ(x^u_i )$ 由特征提取器获得,然后计算其与每个原型的距离如下:
$d_{ik}=d\left{f_\varphi(x_i^u),C_k\right}$
其中,$x^u_i$ 是未标记的样本,$C_k$ 是类别 $k$ 的原型,$d{x_1, x_2}$ 选定为欧氏距离:$d{x_1, x_2} = ∥x_1 - x_2∥^2_2$,$d_{ik}$ 越小表示未标记的样本 $x^u_i$ 越接近类别$k$。
根据计算出的 $d_{ik}$,可以通过公式 (4) 重新定义新的距离 $D_{ik}$,然后形成所有原型的距离矩阵,表示为 $D_i = [D_{i1}, D_{i2}, … , D_{ik}, … , D_{iN} ]$。
$D_{ik}=\frac{d_{ik}}{\min_{j\neq k}d_{ij}+\delta},$
其中 $min_{j \neq k} d_{ij}$ 表示除 $d_{ik}$ 以外的最小距离,$δ = 10^{-8}$ 作为 $min_{j \neq k} d_{ij}$为零时的应急值。
接下来,我们通过以下判别式设计了 LAS:
$\left.y_i^u=\left{\begin{array}{ccc}\arg\min D_i&&if&&\min\left{D_i\right}<\beta\k&&&&else\end{array}\right.\right.$
其中,$y^u_i$ 是分配的伪标签,阈值参数 $β$ 用于控制无标签样本的严格程度,$β$ 越小表示筛选越严格。
根据公式 (4) 和 (5),对于每个未标记样本 xu i,当它特别靠近其中一个原型而远离其他所有原型时,应将未标记的分布内(ID)样本筛选出来并赋予伪标记。当它靠近两个或更多原型,或远离所有原型时,我们将这类未标记样本视为 OOD 干扰样本,并将其剔除。
例如,图 2 展示了在混合了未知未标记样本的 3 类分类任务中设计的 LAS,其中类别分别为 1、2 和 3,生成的带标记样本原型分别为 C1、C2 和 C3。所设计的 LAS 可以充分利用隐藏在未标记样本中的有用信息,并能进一步抑制未知 OOD 样本的干扰。
Scalable-distance-metric-function definition
标准 ProNet 的度量能力相对有限,无法灵活评估样本间的相似性。对图像数据集的最新研究表明,在 ProNet 的距离度量中引入缩放因子可以改善与 Softmax 函数的交互,进一步促进特征聚类和样本分类效果 [36]。受这些研究结果的启发,并考虑到目前用于故障诊断的 ProNet 中距离度量的局限性,我们定义了一种可扩展的距离度量函数,以灵活评估故障样本之间的相似性,并充分提取整个诊断任务空间的通用特性。
在度量函数中加入缩放因子后,可缩放距离度量函数 $\hat{d}{ik}$ 和查询集的预测概率 $P{φ,α}(y = k |x )$ 重写为:
$\begin{aligned}&\hat{d}{ik}=\alpha\cdot d\left{f{\varphi}(x_i^u),C_k\right};\&P_{\varphi,\alpha}(y=k\left|x\right|)=\frac{\exp\left[-\alpha\cdot d\left{f_{\varphi}(x_i^q),C_k\right}\right]}{\sum_{j=1}^N\exp\left[-\alpha\cdot d\left{f_{\varphi}(x_i^q),C_j\right}\right]},\end{aligned}$
其中,α 是缩放因子。根据可扩展的距离度量函数,可以得出所有类别的总损失。
$\begin{aligned}J_k(\varphi,\alpha)&=\sum_{x_i\in\mathbb{Q}k}(\hat{d}{ik}+\log\sum_{j=1}^N\exp(-\hat{d}{ij}));\J(\varphi,\alpha)&=\sum{k=1}^NJ_k(\varphi,\alpha),\end{aligned}$
其中,$Q_k$ 表示类别 k 下的查询集样本,$J_k(φ, α)$ 是类别 k 下所有样本的损失,$J(φ, α)$ 是所有类别下的总损失。
最后,使用随机梯度下降(SGD)优化器更新公式 (7) 中特征提取器的可学习参数 φ 如下。
$\frac{\partial J_k(\boldsymbol{\varphi},\alpha)}{\partial\boldsymbol{\varphi}}=\alpha\cdot\sum_{x_i\in\mathbb{Q}k}\left[\frac{\partial d{i\boldsymbol{k}}}{\partial\boldsymbol{\varphi}}-\frac{\sum_{j=1}^N\exp(-\hat{d}{\boldsymbol{i}j})\frac\partial{\partial\boldsymbol{\varphi}}d{\boldsymbol{i}j}}{\sum_{j=1}^N\exp(-\hat{d}_{\boldsymbol{i}j})}\right]$
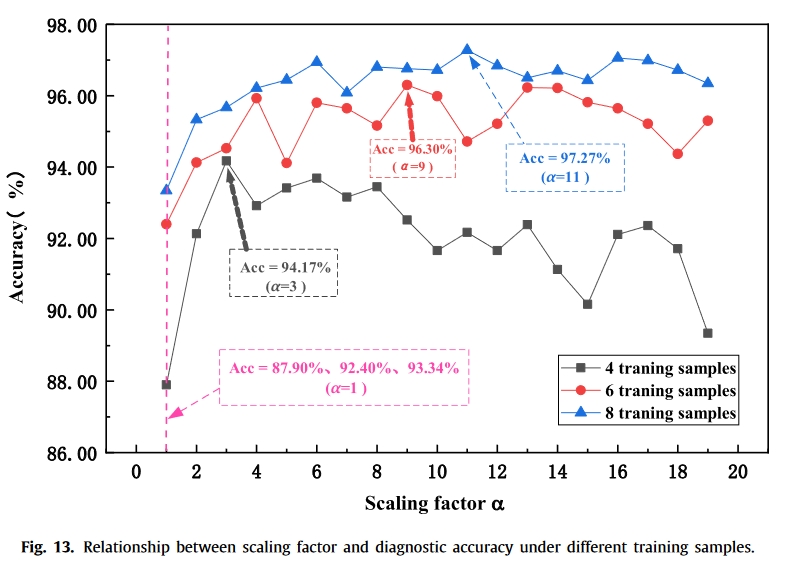
一般来说,当比例因子增加时,故障诊断的分类准确性会提高,错误分类的故障样本数量也会减少。不过,这也会导致平均有效批量大小的减少 [36]。因此,缩放因子的选择取决于具体任务。
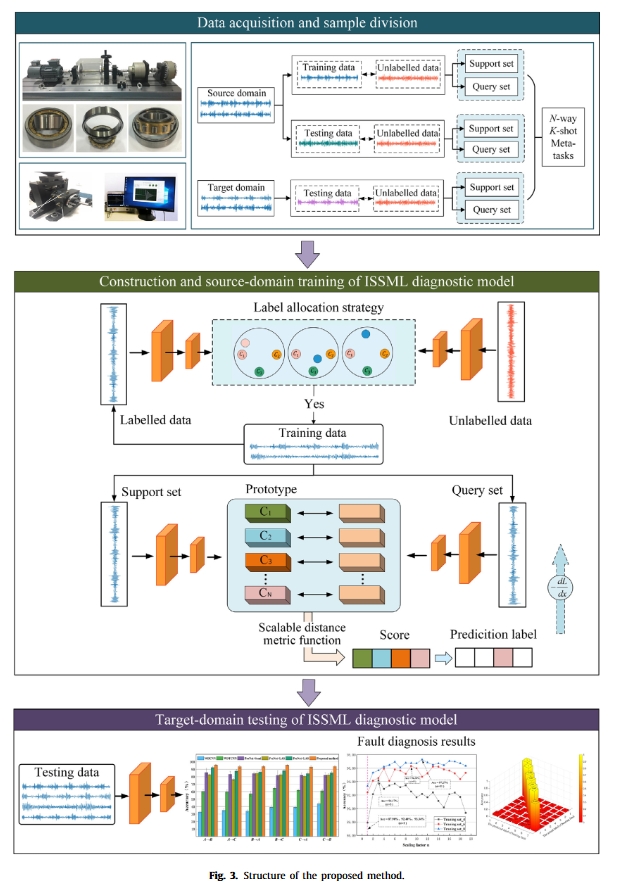
实验
数据集
- M. Jia, J. Wang, Z. Zhang, B. Han, Z. Shi, L. Guo, W. Zhao, A novel method for diagnosing bearing transfer faults based on a maximum mean discrepancies guided domain-adversarial mechanism, Meas. Sci. Technol. 33 (1) (2021) 015109.
在案例研究中,表 1 详细描述了 ID 样品和 OOD 样品的三个等级,其中数据集 A0、B0 和 C0 是在三种速度下采集的少数标记样本,每个数据集包含七个等级:正常状态 (NC)、外圈故障 0.4 毫米 (OF2)、外圈故障 0.6 毫米 (OF3)、内圈故障 0.4 毫米 (IF2)、内圈故障 0.6 毫米 (IF3)、滚子元件故障 0.4 毫米 (RF2) 和滚子元件故障 0.6 毫米 (RF3)。与数据集 A0、B0 和 C0 不同的是,数据集 A1、B1 和 C1 是无标记的,其中混合了三类 OOD 干扰样本,即 0.2 毫米的外环故障 (OF1)、0.2 毫米的内环故障 (IF1) 和 0.2 毫米的滚子元件故障 (RF1)。

超参数/网络
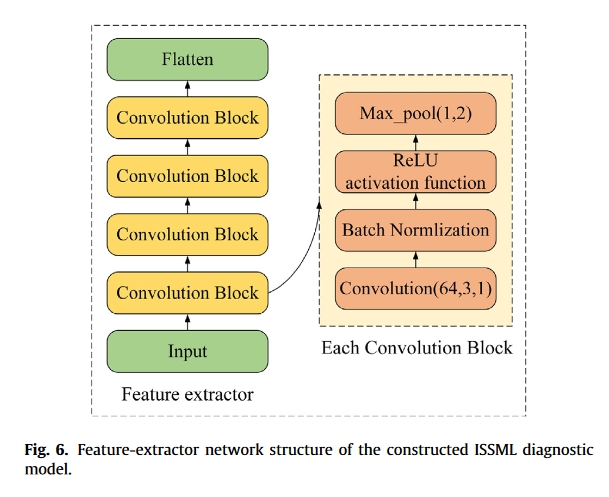
我们方法中的特征提取器网络结构如图 6 所示,由四个卷积模块构成。每个模块由一维 64 滤波器 3 × 1 卷积层、批量归一化层、整流线性单元(ReLU)激活函数层和 1 × 2 最大池化层组成。所有实验均使用英特尔酷睿 i5-10400F CPU、英伟达™(NVIDIA®)GeForce GTX 1650 GPU、16GB 内存,并在 Pytorch-Gpu1.4.0 (Python 3.6) 下运行。在源域训练阶段,迭代次数为 100 次,每次迭代训练 30 个 “七路一枪 “元任务。初始学习率设为 0.1,动量因子设为 0.9,缩放因子 α 设为 7,LAS 中的筛选标准 β 设为 0.01,优化器为 SGD。在目标域测试阶段,每次评估的结果取 200 个 “7 向 1 射 “元任务的平均值。
对比方法
- deep convolutional neural networks with wide first-layer kernels (WDCNN)-2017-Sensor
- deep transfer convolutional neural networks with wide first-layer kernels (WDTCNN)-2017-Adv. Neural Inf. Process. Syst
- ProNet
- ProNet + SSL
- ProNet + LAS

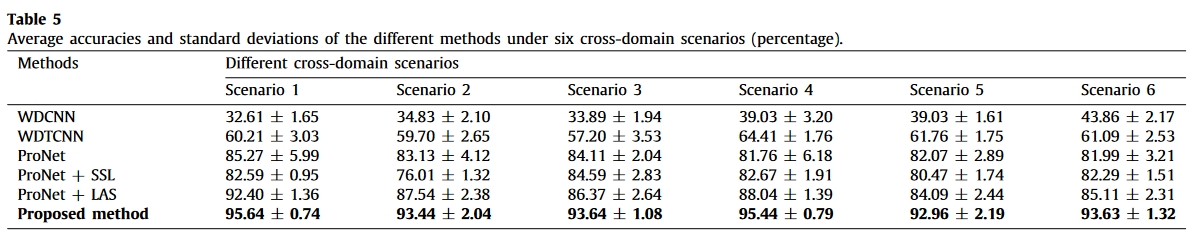
结果

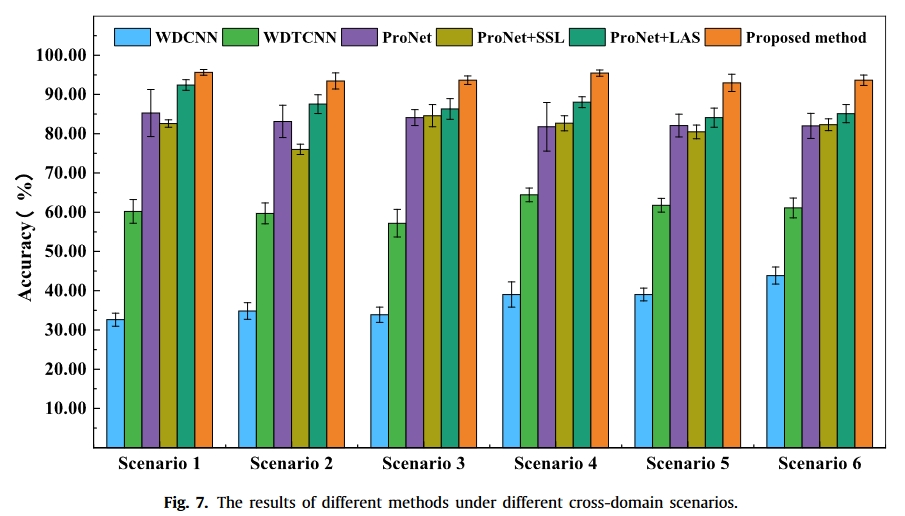
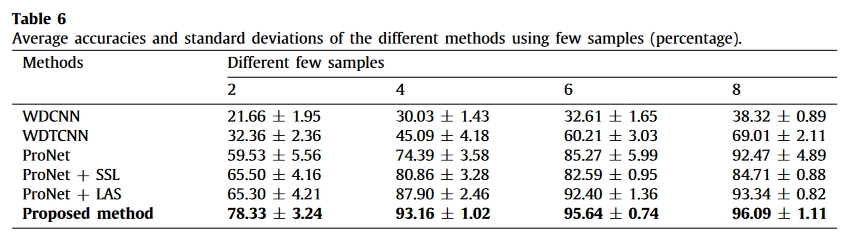
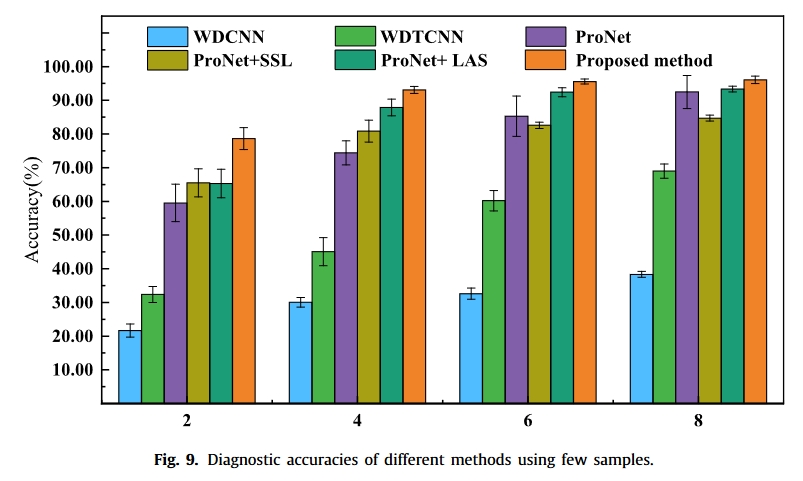
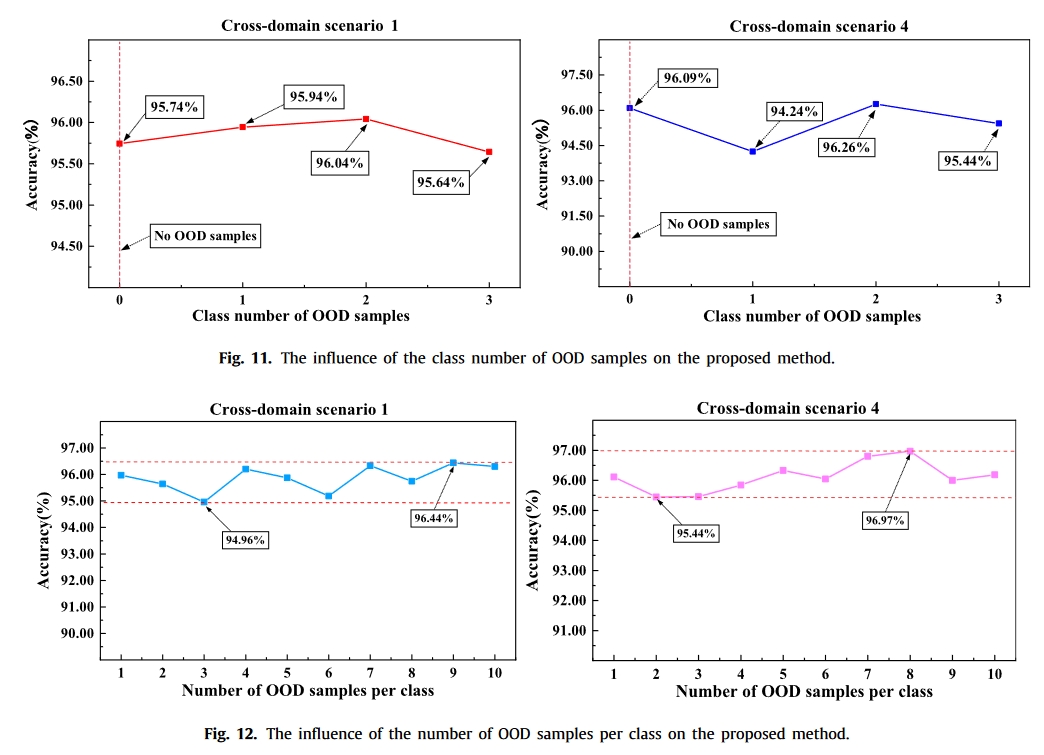
总结
- 使用了元学习来进行故障诊断。
- 提出了一种新的伪标签方案。
- 提出了一种新的可扩展距离度量函数定义(其实只加了一个缩放因子)。