创新点

1. 为了克服全局自适应和单一边际分布匹配的局限性，提出了一种名为 LJMMD 的新型距离度量。提出的 LJMMD 将子域适应的思想融入 JMMD，并采用多核策略来增强算法的鲁棒性。
2. 通过将提出的 LJMMD 作为目标函数嵌入到深度架构中，开发出一种名为 SACNet 的新型迁移学习模型。SACNet 使利用无标记数据训练可靠的故障诊断模型成为可能。
3. 在所开发的 SACNet 中，采用了具有向量输出的胶囊网络来替代经典的全连接自适应层，从而使深度迁移学习模型具有更出色的泛化能力。通过多个转移任务验证了所开发方法的优越性。

相关技术

域泛化

作为 DTL 的代表算法之一，域适应致力于最小化源域和目标域之间的分布差异。对于源域$\mathscr{D}{s}={(\mathbf{x_i^s},\mathbf{y_i^s})}{\mathrm{i}=1}^{\mathrm{n}s}$（包含 ns 个标记样本）和目标域$\mathscr{D}{t}={(\mathbf{x_i^t},\mathbf{y_i^t})}{\mathrm{i}=1}^{\mathrm{n}t}$（包含 nt 个未标记样本），假设$\mathscr{D}{s}$ 和 $\mathscr{D}{t}$ 分别服从分布 p 和 $q(p\neq q)$。域适应的目的是构建一个深度学习分类器$y=f(x)$，学习共享特征并最小化分布差异，从而提高目标域的准确率。域适应的目标函数可以用公式表示。

$\min_f\frac1{n_s}\sum_{i=1}^{n_s}J(f(x_i^s),y_i^s)+\lambda\hat{d}(p,q)$

其中，$J(\cdot, \cdot)$为交叉熵损失，$\hat{d}(\cdot, \cdot)$为域适应损失，$\lambda > 0$ 为权衡参数。

联合最大平均差异(Joint maximum mean discrepancy, JMMD)

在各种域适应损失中，JMMD 是最常用的一种。与之前的其他 MMD 变体相比，JMMD 的优势在于它侧重于数据的联合分布（而非边际分布）。JMMD 及其无偏估计可分别由式（2）和式（3）给出[24]。

$\begin{aligned}
&d_H(p,q)\triangleq && |E_p\left[\otimes_{l=1}^{|L|}\phi^l(z^{sl})\right]-E_q\left[\otimes_{l=1}^{|L|}\phi^l(z^{tl})\right]|{\otimes{l=1}^{|L|}H_k^l}^2 \
&\hat{\boldsymbol{d}}H(\boldsymbol{p},\boldsymbol{q})&& =\parallel\frac1{n_s}\sum{z_i^{sl}\in D_s}\otimes_{l=1}^{|L|}\phi^l(z_i^{sl})-\frac1{n_t}\sum_{z_j^{tl}\in D_t}\otimes_{l=1}^{|L|}\phi^l(z_j^{tl})\parallel_{\otimes_{l=1}^{|L|}H^l}^2 \
&&&=\frac1{n_s^2}\sum_{i=1}^{n_s}\sum_{j=1}^{n_s}\prod_{l\in L}k^l(z_i^{sl},z_j^{sl}) \
&&&+\frac1{n_t^2}\sum_{i=1}^{n_t}\sum_{j=1}^{n_t}\prod_{l\in L}k^l(z_i^{tl},z_j^{tl}) \
&&&-\frac2{n_sn_t}\sum_{i=1}^{n_s}\sum_{j=1}^{n_t}\prod_{l\in L}k^l(z_i^{sl},z_j^{tl})
\end{aligned}$

其中，$\otimes_{l=1}^{|L|}\phi^l(x^l)=\phi^1(x^1)\otimes\cdots\otimes\phi^{|L|}(x^{|L|})$ 表示张量乘希尔伯特空间中的特征映射，L 是较高网络层的集合，|L| 是相应集合中的层数、$Z^{sl}$ 是第 l 层的源域输出，$Z^{tl}$ 是第 l 层的目标域输出，H 是重现核希尔伯特空间（RKHS），$\phi(\cdot)$是将原始数据转换为 RKHS 的映射，$k(X^s,X^t)=\langle\phi(X^s),\phi(X^t)\rangle$。

方法

提出的局部联合最大均值差异

虽然联合分布的引入使得 JMMD 比其他只关注边际分布的 MMD 变体更具优势，但在联合分布的匹配过程中，JMMD 仍然是一种全局匹配，没有考虑不同子类的分布。因此，它可能会导致源域和目标域中不同子类之间的混淆，最终降低域适应的性能。本节将参考文献[27]中的子域自适应思想引入 JMMD，以匹配数据在子域层面的联合分布。

具体而言，对于源域$\mathscr{D}{s}={(\mathbf{x_i^s},\mathbf{y_i^s})}{\mathrm{i}=1}^{\mathrm{n}s}$和目标域$\mathscr{D}{t}={(\mathbf{x_i^t},\mathbf{y_i^t})}{\mathrm{i}=1}^{\mathrm{n}t}$。假设$\mathscr{D}{s}$和$\mathscr{D}{t}$可以分别分为C子域$\mathscr{D}^{(c)}{s}$和$\mathscr{D}^{(c)}{t}$，$\mathscr{D}^{(c)}{s}$和$\mathscr{D}^{(c)}{t}$服从分布$p^(c)$和$p^(c)(p^{(c)} \ne q^{(c)})$。子域自适应的目的是构建一个深度学习分类器$y=f(x)$来学习相应子域之间的共享特征，并最大限度地减少联合分布差异。子域自适应的目标函数可以由下面的公式给出。

$\min_f\frac1{n_s}\sum_{i=1}^{n_s}J(f(x_i^s),y_i^s)+\lambda E_c\left[\hat{d}(p^{(c)},q^{(c)})\right]$

其中，$J(\cdot, \cdot)$为交叉熵损失，$\hat{d}(\cdot, \cdot)$为域适应损失，$\lambda > 0$ 为权衡参数，$E_c[\cdot]$表示数学期望。

根据公式(4)中的子域思想重写公式(2)，LJMMD 可由公式(5)给出。

$d_H(p,q)\triangleq E_c\parallel E_{p^{(\mathfrak{c})}}\left[\otimes_{l=1}^{|L|}\phi^l(z^{\mathfrak{s}l})\right]-E_{q^{(\mathfrak{c})}}\left[\otimes_{l=1}^{|L|}\phi^l(z^{tl})\right]\parallel_{\otimes_{l=1}^{|U|}H_k^l}^2$

假设每个样本根据权重 wc 属于每个类别，公式 (5) 的无偏估计值由公式 (6) 给出。

$\begin{aligned}
\hat{\boldsymbol{d}}H(p,\boldsymbol{q})& =\frac1C\sum{c=1}^{\mathbb{C}}|\sum_{\boldsymbol{z}i^{sl}\in D_s}\boldsymbol{w}i^{\mathrm{sc}}(\otimes{l=1}^{|L|}\phi^l(\boldsymbol{z}i^{sl}))-\sum{\boldsymbol{z}j^{tl}\in D_t}\boldsymbol{w}j^{t\mathbf{c}}(\otimes{l=1}^{|L|}\phi^l(\boldsymbol{z}j^{tl}))|{\otimes{l=1}^{|L|}H^l}^2 \
&=\frac1C\sum{c=1}^C\left[\sum_{i=1}^{n_s}\sum_{j=1}^{n_s}w_i^{sc}w_j^{sc}\prod_{l\in L}k^l\left(z_i^{sl},z_j^{sl}\right)\right. \
&+\sum_{i=1}^{n_t}\sum_{j=1}^{n_t}w_i^{tc}w_j^{tc}\prod_{l\in L}k^l\left(z_i^{tl},z_j^{tl}\right) \
&-2\sum_{i=1}^{n_s}\left.\sum_{j=1}^{n_t}w_i^{sc}w_j^{tc}\prod_{l\in L}k^l\left(z_i^{sl},z_j^{tl}\right)\right]
\end{aligned}$

其中，$\otimes_{l=1}^{|L|}\phi^l(x^l)=\phi^1(x^1)\otimes\cdots\otimes\phi^{|L|}(x^{|L|})$表示在张量乘希尔伯特空间中的特征映射，L 是一个高级网络层集合，$|L|$ 是相应集合中的层数，$Z^{sl}$ 是第 l 层的源域输出，$Z^{tl}$ 是第 l 层的目标域输出，H 是 RKHS，$\phi(\cdot)$是可以将原始数据转换为 RKHS 的映射，$k(X^s,X^t)=\langle\phi(X^s),\phi(X^t)\rangle$；$w^{sc}_i$ 和 $w^{tc}_j$ 分别代表属于 c 类的 $x^s_i$ 和 $x^t_j$ 的权重。

$w_i^c=\frac{y_{ic}}{\sum_{(x_i,y_i)\in D}y_{ic}}$
其中，$y_{ic}$ 是向量 $y_i$ 的第 c 个条目，$w^{sc}_i$ 可以根据源域数据的真实标签计算，而 $w^{tc}_j$ 可以根据预测标签和目标域数据计算。

此外，为了减少所提出的 LJMMD 在选择核函数和相应参数时的主观性，采用了多核函数组合的方法来增强算法的鲁棒性，多核策略可用式（8）表示。

$K\triangleq\left{k=\sum_{u=1}^m\beta_uk_u:\sum_{u=1}^m\beta_u=1,\beta\geqslant0,\forall u\right}$

其中，$\beta_u$ 表示不同内核的权重。

对于源域$\mathscr{D}{s}={(\mathbf{x_i^s},\mathbf{y_i^s})}{\mathrm{i}=1}^{\mathrm{n}s}$（包含 ns 个标记样本）和目标域$\mathscr{D}{t}={(\mathbf{x_i^t},\mathbf{y_i^t})}{\mathrm{i}=1}^{\mathrm{n}t}$（包含 nt 个未标记样本）。本工作中的子域联合分布适应的目的是将$\mathscr{D}{s}$和$\mathscr{D}{t}$分成 C 个子域$\mathscr{D}^{(c)}{s}$和$\mathscr{D}^{(c)}{t}$ ，C 代表子域的类别），并构建一个深度学习分类器来学习源域和目标域中相应子域之间的共享特征。这样就可以减少不同子域之间的联合分布差异，在保证源域分类精度的前提下提高目标域的分类精度。与其他方法相比，本文提出的 LJMMD 在更精细的子域空间中匹配源域和目标域数据的联合分布，可以避免全局匹配或边际分布匹配的盲目性和局限性。此外，多核策略的引入还能进一步降低核函数选择的风险，增强域适应过程的鲁棒性。

提出的 SACNet 的结构

SACNet 的总体结构

在本节中，子域自适应胶囊网络（SACNet）是在LJMMD的基础上开发的。在SACNet中，LJMMD作为目标函数的一部分嵌入到深度网络中，以最小化源域和目标域之间的子域联合分布差异。如图1所示，SACNet主要由骨干、瓶颈和输出层组成。主干模块由几个传统的卷积层构建，其功能是作为整体模型的特征提取器，提取分类和领域自适应所需的高维特征。在瓶颈模块中，有一个自适应层，其主要功能是匹配源数据和目标域的联合分布。在SACNet的末端，使用全连接层作为分类层。此外，SACNet中的所有参数都由源域数据和目标域数据共享。

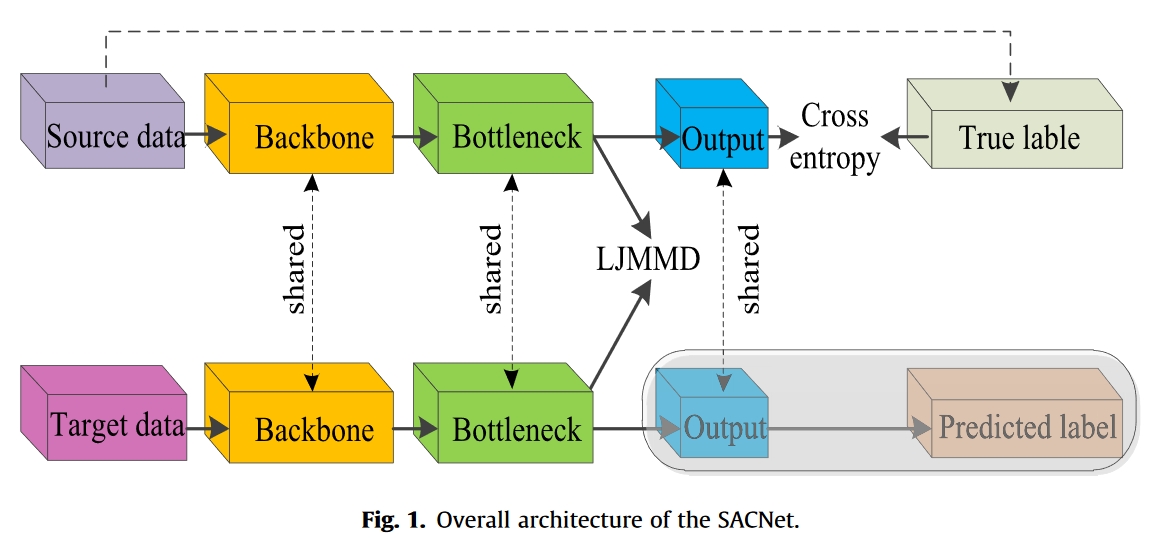
向量化胶囊适应层

为了兼顾差异性和一致性，所开发的 SACNet 利用胶囊网络[28] 取代了经典的全连接自适应层。具体来说，本文将主干网中最后一个卷积池化单元输出的特征图视为主要胶囊（PCaps），因此 PCaps 的数量等于特征图的通道数，PCaps 的维数与特征图的维数相同。

如图 2 所示，在得到 i 个 PCaps 向量后，就可以在胶囊层中计算出 DigitalCaps（DCaps）向量，PCaps 到 DCaps 的转换过程可以用公式 (9)、公式 (10) 和公式 (11) 来描述。

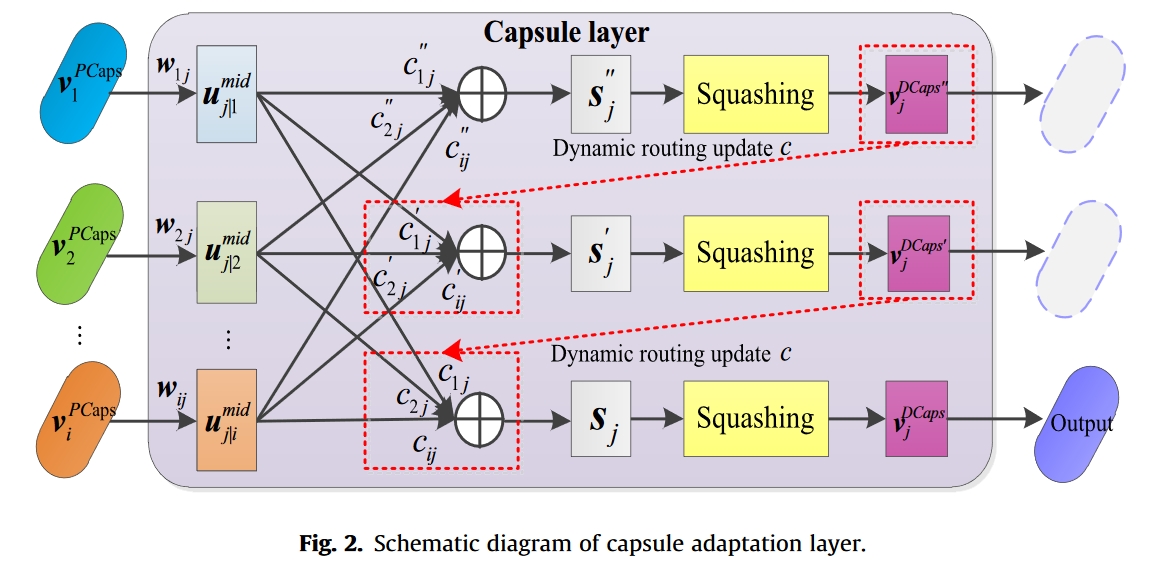
$\begin{aligned}
&\boldsymbol{u}{j|i}^{mid}=\boldsymbol{w}{ij}\boldsymbol{v}i^{PCaps} \
&\boldsymbol{s_j}=\sum_ic{ij}\boldsymbol{u_{j|i}^{mid}} \
&\boldsymbol{v}_j^{D\boldsymbol{Caps}}=\operatorname{Squashing}(\boldsymbol{s}_j)
\end{aligned}$

其中，vPCaps i 是 PCaps 向量，$w_{ij}$ 是变换矩阵，$u^{mid}{j|i}$ 表示中间预测向量，$s_j$ 是所有中间预测向量的加权和，$c{ij}$ 是耦合系数，$v^{SCaps}_j$ 是 DCaps 向量，Squashing 是激活函数，可以用下面公式来定义。

$\mathrm{Squashing}(t)=t|t|/\left(1+|t|^2\right)$

模型优化

子域联合分布自适应的目标是构建深度学习分类器，学习相应子域之间的共享特征，在保证源域准确率的前提下提高目标域的准确率。因此，SACNet 的目标函数主要由两项组成，包括用于分类的传统交叉熵损失和用于分布匹配的域自适应损失（LJMMD）。总的来说，SACNet 的训练过程可分为两个阶段：预训练和转移训练。图 3 显示了 SACNet 的训练过程，表 1 列出了详细的伪代码。

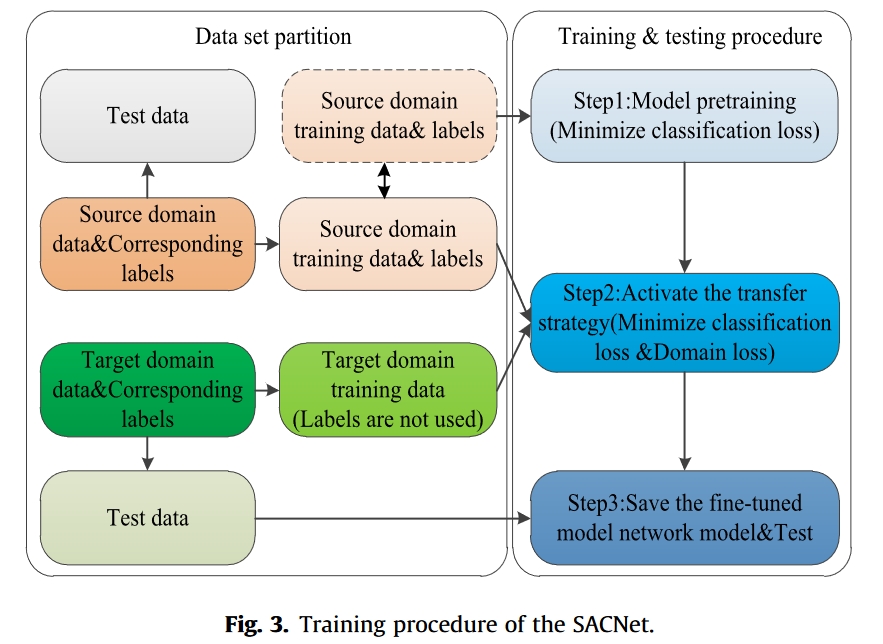
在预训练阶段，SACNet 只输入已标注的源域数据，网络训练的目标是最小化源域的分类损失。在这一阶段，SACNet 与传统分类模型无异，其优化目标可由下式给出。

$\min_f\frac1{n_s}\sum_{i=1}^{n_s}J(f(x_i^s),y_i^s)$

其中$J(\cdot, \cdot)$表示交叉熵。

经过一定次数的迭代训练后，源域的交叉熵损失将优化到一个相对较低的水平。此时，SACNet 将启动迁移策略，迁移学习的目标是最小化源域和目标域之间的 LJMMD。当不同域之间的 LJMMD 降低到一定程度时，能准确识别源数据的模型也能在一定程度上识别目标域数据。下面是最终损失函数。

$\min_f\frac1{n_s}\sum_{i=1}^{n_s}J(f(x_i^s),y_i^s)+\lambda\hat{d}_{LJMMD}(p,q)$

其中$J(\cdot, \cdot)$是交叉熵，$\hat{d}_{LJMMD} (\cdot, \cdot)$是子域联合分布损失，$\lambda>0$是权衡参数。

实验

超参数/网络

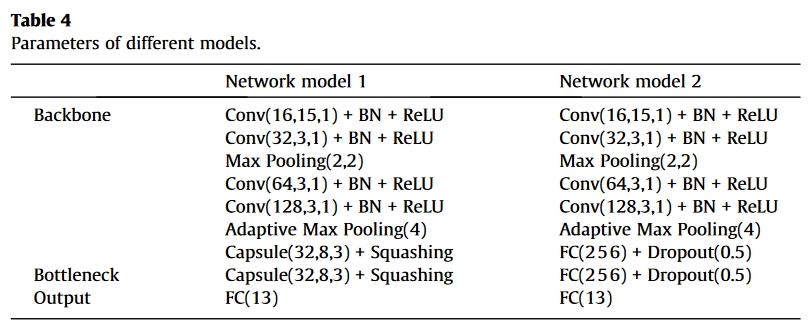
在训练阶段，epoch被设置为300。值得注意的是，在前50个epoch中，只使用标记的源域数据，目的是获得一个预训练的模型，该模型可以完成源域的分类任务。在得到预先训练的模型后，转移策略将被激活（51到300epoch）。为了加速模型收敛和节省计算机内存，采用了小批量训练模式，批量大小设置为32。Adam被设置为优化算法（初始学习率为0.001，在150和250epoch时将分别降低到前一阶段的十分之一）。此外，本工作采用渐进式训练方法，在激活转移策略后，将权衡参数s从0增加到1。

数据集

1. Paderborn University bearing dataset
2. PHM2009 gearbox dataset

对比方法

1. wasserstein distance based deep transfer learning method (WD-DTL)-2020-Eenurocomputing
2. JMMD with adversary strategy-2020-Mech. Syst. Signal Process
3. CORAL with adversary strategy-2021-Measurement
4. LMMD-2021-IEEE Trans. Neur. Net. Lear.
5. MK-LMMD-2021-IEEE Trans. Instrum. Meas.
6. JLMMD-2022-IEEE Sensors Journal

结果

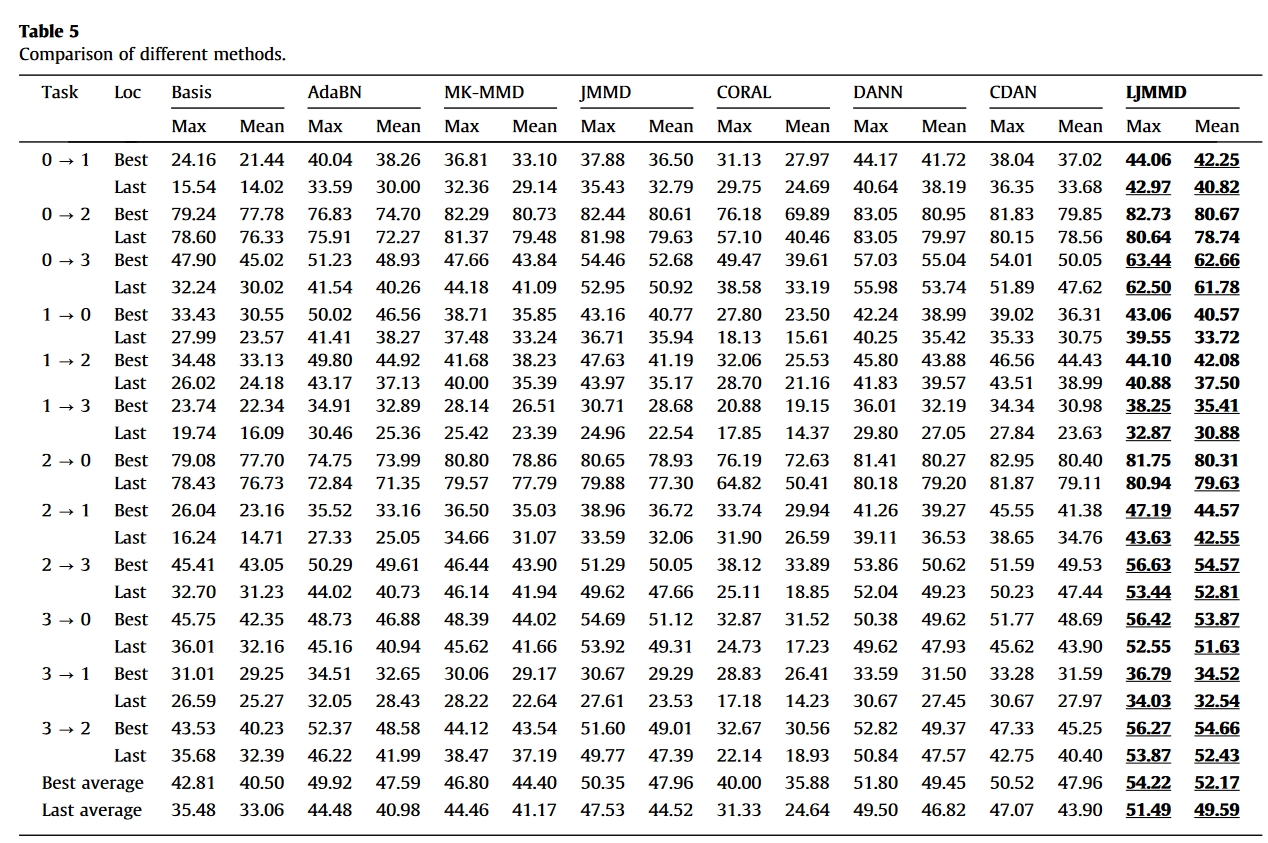
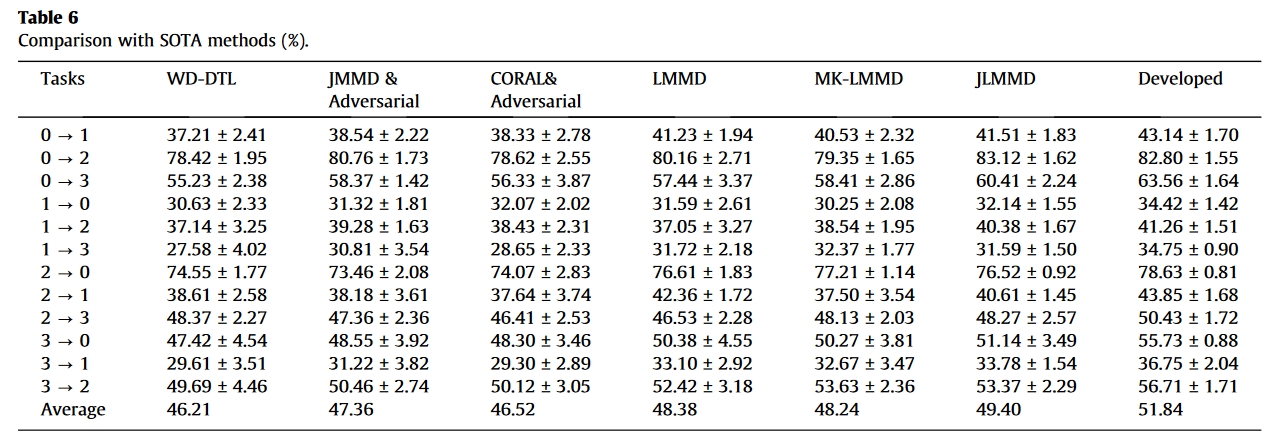
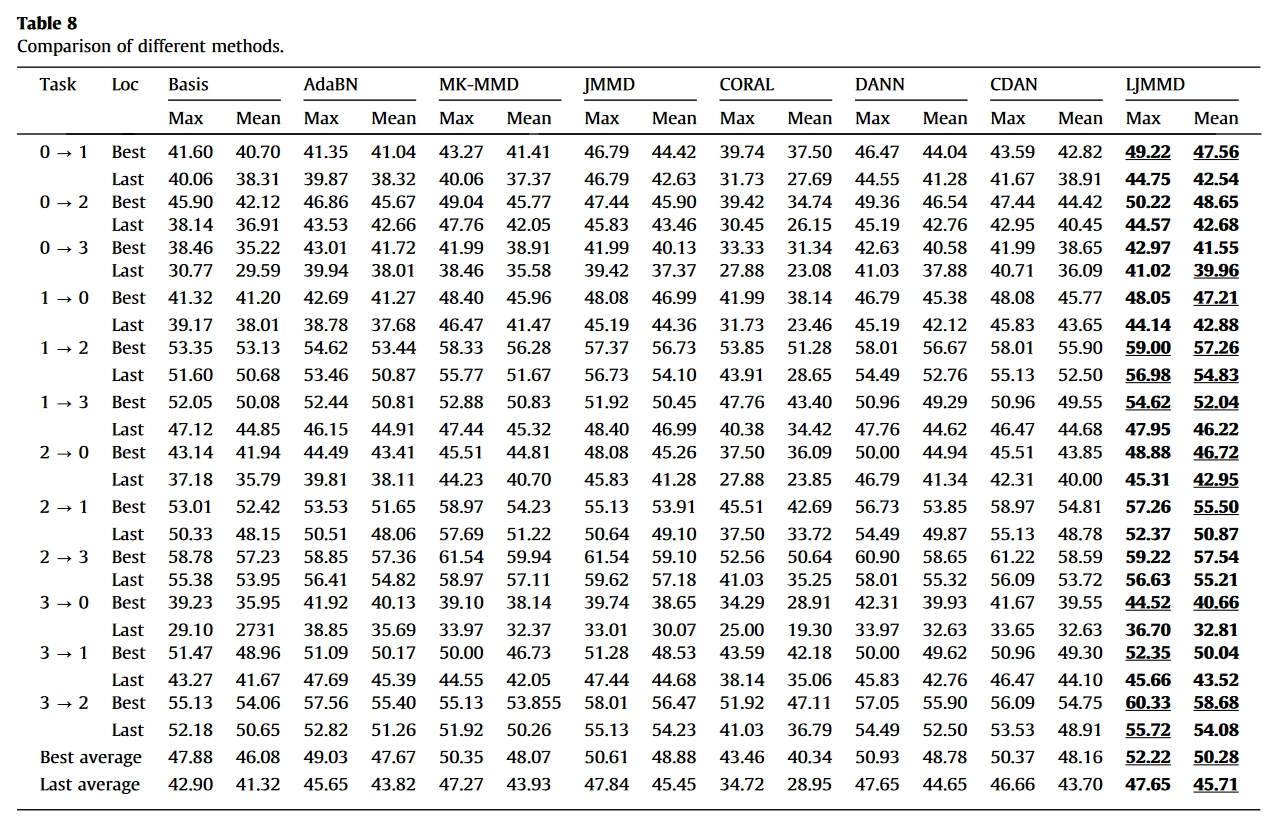
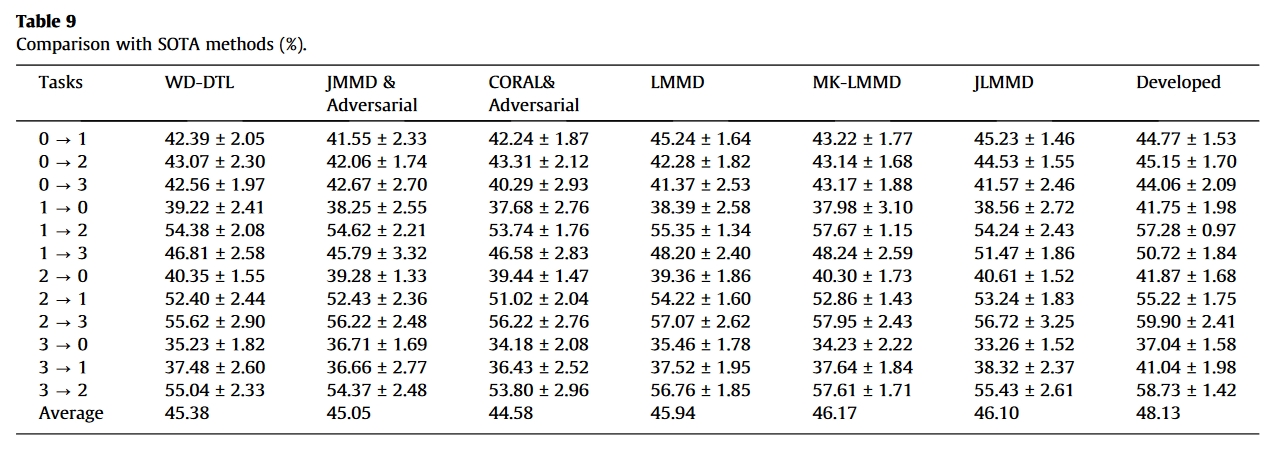
总结

本文的主要创新点有两个：

1. 提出了LJMMD，其实算是加了子域的权重。
2. 提出使用胶囊网络替代全连接层。

另外还是用预训练微调的方法来训练模型，使得训练结果更好。

关于迁移学习，还要了解其最新改进。

[27] Y.C. Zhu, F.Z. Zhuang, J.D. Wang, Deep subdomain adaptation network for image classification, IEEE Trans. Neur. Net. Lear. 32 (4) (2021) 1713–1722.