期刊: Advanced Engineering Informatics (IF:8.8)
引言
旋转机械在工业设备中至关重要,但长期运行会导致性能下降。为了确保安全和提高可靠性,需要准确诊断关键部件的健康状况。传统的信号处理方法已无法满足需求,因此基于深度学习算法的智能故障诊断方法受到了关注。这种方法可以自适应地提取原始信号的深层特征,从而提高故障检测的效果。
深度学习方法需要大量平衡的样本来完成模型训练,但实际工业生产中不同健康条件下获得的故障信号非常稀缺和不平衡。这导致包含故障信息的样本非常有限,容易出现过拟合效应,影响故障诊断的准确率和模型泛化能力。同时,获得具有完整类别的标记故障样本需要高昂的经济成本和人力消耗。这些问题严重影响了机械故障诊断的效果。
研究人员从不同角度解决了小样本下的机械故障诊断问题。目前主要有下面的研究点:
- 传统数据综合方法:过采样。
- 机器学习方法。
采样技术是故障诊断领域常用的数据增强方法。然而,这种方法的增强效果仅仅停留在数据层面。它通过对真实信号的线性插值生成新信号,并不能深入挖掘信号的深层特征和分布规律。
此外,该方法还可能产生不正确或不必要的样本,无法扩大样本的多样性。
因此,基于深度学习的数据增强方法在故障诊断中是一种很有前途的解决方案,它能满足高质量均衡训练集的要求。
介绍了GAN网络。
介绍了GAN网络在故障诊断中的一些应用。
然而GAN网络存在一些问题:
- 难以训练:鉴别器通常比生成器训练得更好,很容易区分真假样本,从而为生成器提供无信息的梯度。有效平衡生成器和鉴别器的性能很重要,但也很困难,因为精度很高的鉴别器会产生信息量相对较少的梯度,但精度较低的鉴别器也可能会阻碍生成器的学习能力。
- 模式坍塌:指合成的样本都趋同;
为了解决上述问题,提出了下面的方法:
- 针对数据生成和故障分类,提出了一种小样本下的新型故障诊断方法。将编码器纳入鉴别器,提取原始样本的重要表征,构建了一个包括编码器、生成器和鉴别器的增强网络。然后生成真实的故障样本来增强原始的不平衡样本,从而提高小样本下的故障诊断效果。
- 提出了一种变异信息约束,利用形成瓶颈法提高生成对抗结构的训练稳定性。通过对输入信号和判别器深度特征之间的互信息施加约束,鼓励判别器学习输入信号和生成器分布之间重合度高的深度特征,从而有效地调节判别器的精度,保持有用的信息梯度。鉴别器对发生器的反馈梯度会自动调整,进一步促进深度网络结构的稳定训练和快速收敛。
- 为了解决模式崩溃问题,网络中加入了表征匹配模块。表征匹配模块计算生成信号的深层特征与鉴别器每个中间层的真实信号之间的分布差异。该差值作为目标函数的一部分,用于对生成器施加限制,促进生成的样本覆盖多类输入数据集的每个子类,从而提高合成样本的多样性。
相关工作
下面的内容见Multi-mode-data-augmentation-and-fault-diagnosis-of-rotating-machinery-using-modified-ACGAN-designed-with-new-framework。
GAN
Wasserstein GAN with gradient penalty
WGAN通过在生成对抗性网络中引入Wasserstein距离来代替Kullback-Leibler(KL)散度和Jensen–Shannon(JS)散度,可以防止生成器可能的梯度消失,并且训练过程更加稳定。
然而,当WGAN处理Lipschitz连续性约束时,由于深度学习模型的多层结构和训练方法,简单的权重裁剪方法会引起问题。
- 缺陷是权重裁剪的值可能导致鉴别器中的梯度问题。由于多层神经网络使权重裁剪阈值在多层中传播,因此梯度值将呈指数级增加或衰减。在实际应用中要找到这样一个平衡区域并不容易。
- 权重裁剪将参数限制在特定的范围内,使得鉴别器的所有参数都是有界的,这确保了训练的稳定性。然而,这与鉴别器的训练目标相冲突。鉴别器希望通过训练尽可能地放大真实样本和伪样本之间的差异,这导致鉴别器的所有参数值都倾向于设置区间的边缘,无法充分利用神经网络强拟合能力的优势。
为了解决上述问题,Gulrajani 提出了 WGAN-GP,用梯度惩罚项代替权重剪切。这种新模型不仅符合 Lipschitz 限度,而且缓解了 WGAN 中的参数集中和梯度消失或爆炸问题 。WGAN-GP 的目标函数如下。
$L(G,D)=\underset{G}{\operatorname*{minmax}}E_{x\sim P_{da}}[D(x)]-E_{y\sim P_{8}}[D(y)]-\lambda E_{r\sim P_{r}}[\left(||\nabla_{r}D(r)||_{2}-1\right)^2]$
其中第三项为梯度惩罚项,λ 为惩罚系数,1 为限制梯度值。公式中的 Pr 指的不是整个样本空间,而是 Pda 和 Pg 之间的采样空间。由于对整个样本空间采样所需的样本数是指数级的,在实际应用过程中很难实现,因此我们只需关注原始分布和合成分布以及它们之间的区域。x 和 y 之间的随机插值采样如下。
$r=εx+(1-ε)y$
其中,$x ∼ P_{da}$,$y ∼ P_g$,ε ∼ Uniform[0,1],ε 表示从 0 到 1 的随机变量。
提出的方法
本文介绍了用于小样本机器故障诊断的变异信息约束生成式对抗网络。所提出的方法包含三个模块:深度特征的变分信息约束、生成式对抗网络的新损失函数设计以及所建议网络的一般程序。
深度特征的变异信息约束
有效稳定生成式对抗结构的训练过程非常重要。为了更好地促进 GAN 模型的稳定性,保持判别器梯度的有效性,在判别器中采用了变异信息约束技术。
在传统 GAN 的训练阶段,如果判别器训练不足,生成器将无法获得判别器反馈的准确引导信息。但是,如果判别器训练得太好,就会导致发生器的梯度学习问题。判别器的梯度控制成为对抗模型训练的关键。为了解决梯度问题,有两种常见的解决方案:一种方法是在模型的隐藏层中加入误差,这样真实样本和虚假样本的分布就可能存在交集。同时,这将增加判别器区分真假样本的难度,降低梯度消失的可能性。然而,误差对样本分布的影响不易控制,因此判别器和生成器的性能很难达到纳什均衡。
解决梯度问题的另一种方法是对判别器的性能施加额外的约束。一些学者引入了正则化器,如梯度惩罚[36]。与梯度惩罚法类似,本文提出的方法也旨在对判别器进行正则化,以改善对发生器的反馈。不过,与梯度的显式正则化不同,该方法对判别器施加了一个信息瓶颈。通过限制输入样本与判别器内部特征之间的互信息,可以有效地调整判别器的精度,并保持有用的信息梯度。这样,生成器就可以集中精力改善真假样本之间最明显的差异,而不会受到鉴别器传输的错误梯度信息的干扰。
变异信息约束技术基于信息瓶颈,是一种对深度特征进行正则化处理以最小化与输入信号的互信息的方法。受变异自动编码器(VAE)方法的启发,信息瓶颈可通过使用变异约束和重参数化技术应用于深度网络。这种用于稳定对抗学习的自适应正则化方法可被视为实例噪声的一种变体。互信息是衡量两个变量共享信息的指标,它衡量两个变量中一个变量对另一个变量不确定性的降低程度。以变量 X 和 Y 为例。如果 X 和 Y 相互独立,则已知 X 不会为 Y 提供任何信息,反之亦然,因此它们的互信息为零。限制输入数据与判别器深度特征之间的互信息,可以让正则器直接控制判别器的准确性。正则器会自动选择噪声大小,并将噪声应用于输入数据的深度表示。然后对所选噪声进行专门优化,以模拟生成器与数据分布之间最明显的差异。变异信息约束示意图如图 2 所示。编码器将样本映射到潜空间,通过对输入样本和特征之间的互信息施加约束来控制鉴别器的性能,从而提高鉴别器反馈给生成器的梯度的准确性。假设 × 表示输入样本,z 表示编码器 E(z|x) 映射的深度特征,则两个变量之间的互信息 M(x, z) 定义如下:
$M(x,z)=E_{w\sim p_w(x)}[KL[E(z|w)||r(z)]]$
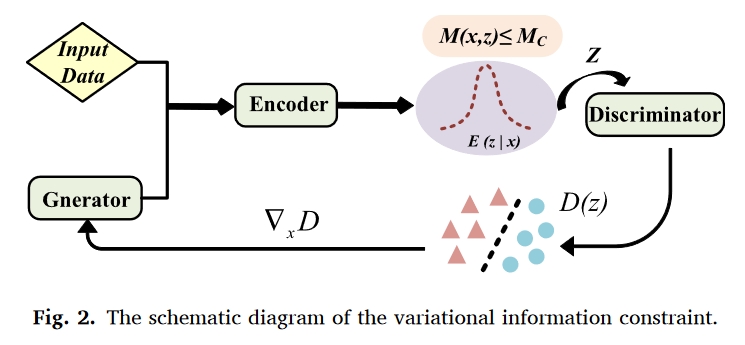
其中,$pw(x)$ 是输入数据的分布,$KL[a||b]$ 表示变量 a 和 b 的 KL 发散。r(z) 由标准高斯分布构建,表示边际的近似值,以获得变异下限。根据变异信息约束技术,对原始样本与特征之间的互信息采用如下的上限 Mc。
变异信息约束法通过对深层特征的约束来调整判别器的性能,要求判别器中间层和输入层的互信息必须小于阈值。使用变异信息约束可以鼓励鉴别器学习真实数据和生成器数据分布之间重叠的特征信息,从而为生成器保持有用的信息梯度。这种技术能使判别器更加关注一些有用的信息,避免无用信息造成的过拟合现象。相关研究表明,这种技术能促使网络忽略无关信息,生成更高质量的样本[39]。
生成式对抗网络的新损失函数设计
除了变异信息约束方法之外,为了缓解模式坍塌和提高样本多样性,还为提出的网络添加了表征匹配模块,并将其作为新目标函数的一部分,对编码器和生成器施加限制。标准的 GAN 框架由一个鉴别器 D 和一个生成器 G 组成。鉴别器的目标是鉴别真实数据 x 和生成器合成的样本 y,如下式所示。
$L(G,D)=\underset{G}{\operatorname*{minmax}}E_{x\sim P_{da}}[\log D(x)]+E_{y\sim P_{s}}[\log(1-D(y))]$
通过在判别器 D 中加入编码器 E,将样本 x 映射到随机编码z ∼ E(z|x),判别器的输入就变成了深度编码信息而不是样本,从而建立了一个具有更强数据合成能力的改进型生成对抗网络。同时,利用变异信息约束技术,对初始样本与编码之间的互信息 M(x, z) 进行 Mc 约束。
然后训练 D 来区分编码分布中的样本,具有互信息约束的判别器的正则化目标如下式。
$\begin{aligned}L_{reyularize}&=\underset{D,E}{\operatorname*{min}}E_{x\sim P_{da}}[E_{z\sim F!(z|x)}[-\log(D(z))]]+E_{y\sim P_s}[E_{z\sim F(z|y)}[-\log(1-D(G(z))]]\&s.t.E_{w\sim p_w(x)}[KL[E(z|w)||r(z)]]\leq M_c\end{aligned}$
其中 $p_w = 0.5Pd_a +0.5P_g$ 表示真实数据集和生成数据集的混合。先验$r(z)= N(0,1)$由标准高斯分布构建,表示边际的近似值,以获得变分下界[40]。编码器 E(z| x)= N(μ(x),v(x))在潜空间 z 中创建一个高斯分布,其均值为 μ(x),方差为 v(x)。在计算 KL 函数时,每批数据包括来自 Pda 和 Pg 的相同数量的样本。为了优化该目标函数,引入了一个拉格朗日乘数 β,优化目标是找到下式的最小值。
$L_{toual}=E_{x\sim P_{da}}[E_{z\sim E(z|x)}[-\log(D(z))]]+E_{y\sim P_s}[E_{z\sim E(z|y)}[-\log(1-D(G(z))]]\+\beta(E_{w\sim p_w(x)}[KL[E(z|w)||r(z)]]-M_c)$
对x和z施加特定的互信息约束对于更好的性能至关重要,因此通过双梯度下降方法自适应更新β,以对互信息施加特定的约束Mc[41]。同时,鉴别器和编码器还根据目标函数的梯度反馈不断更新参数。目标函数中的信息约束是鉴别器的中间隐藏层和输入层之间的相互信息小于某个阈值。信息约束的优点是使鉴别器更加关注一些有用的信息,避免过拟合现象。在GAN网络的训练中,生成器的目的是生成假数据来混淆鉴别器。在模型训练的早期阶段,生成的数据与真实数据之间的分布差距相当大。在这个阶段,鉴别器很容易识别输入数据的来源,导致生成器训练不稳定,生成的数据不令人满意。然而,生成器的梯度精度对于生成对抗性模型的稳定性是重要的。
为了解决模型训练不稳定和模式崩溃的问题,引入了表示匹配方法来增强生成器的损失函数。与最初的GAN模型只取鉴别器网络最后一层的输出不同,表示匹配模块使生成的信号更接近鉴别器每个中间层的真实信号。生成器不断地被训练以学习鉴别器中的多重深度特征,从而随着模型的训练,使生成的样本和真实样本具有更接近的特征表示。因此,表示匹配方法有助于提高生成样本的准确性和多样性,避免模型训练的偏差。当生成的数据的特征中心与真实数据的特征非常匹配时,意味着匹配损失函数值为0,并且生成的数据具有高质量。
表示匹配通过约束公式右半部分的特征来减少真实样本和生成样本之间的距离,并且L2距离是在特征向量的平均值之间测量的。生成器的改进的目标函数可以表示为下式,
$L(G)=-E_{y\sim P_s}[D(\mu(y))]+b\cdot||E_{y\sim P_s}f(y)-E_{x\sim P_n}f(x)||_2^2$
其中KL损失不包括在生成器的目标函数中。对于我们的诊断任务来说,通过在编码器分布的平均μ(x)处计算D而不是在z上计算期望来近似期望就足够了。f(y)和f(x)表示鉴别器的多层中的合成数据和原始数据的特征,b表示表示匹配的可调节因子。
提出方法的框架
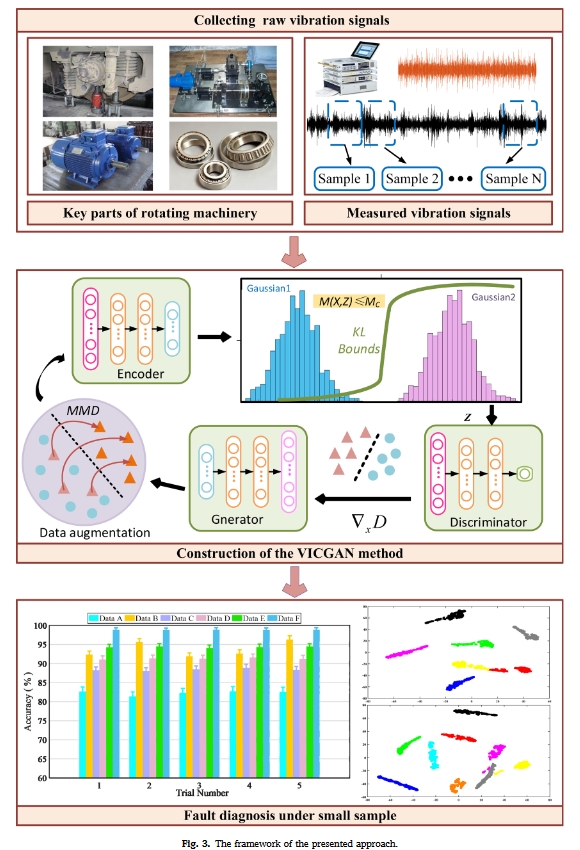
第二部分是所提出的VICGAN方法的构造,该方法由四个神经网络模块组成:
- 编码器:编码器将原始数据映射为潜在编码,并且鉴别器的输入从原始样本改变为包含特征信息的潜在编码
- 鉴别器:所提出的变分信息约束技术可以约束原始数据和潜在编码之间的相互信息,限制鉴别器的梯度,从而获得更稳定的模型
- 生成器
- 变分信息约束模块
同时,使用数据质量评估指标,如最大平均差异(MMD)来筛选生成的数据,以实现真实性。经过上述过程,消除了原始数据集的不平衡。
实验
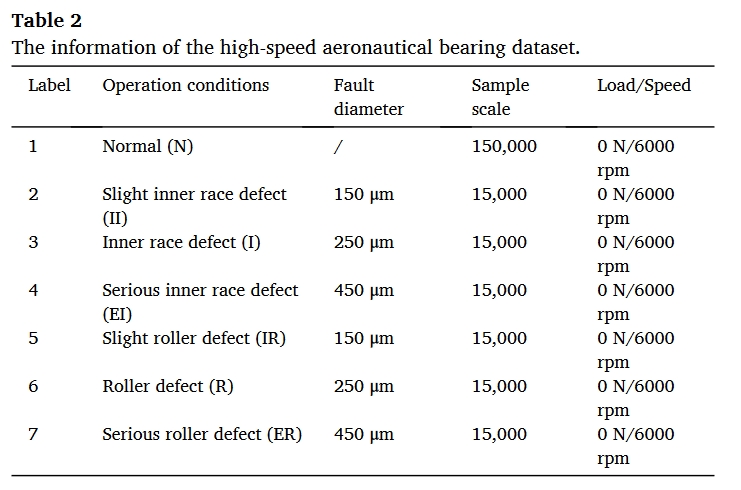
数据集
- eronautical bearing dataset-. Daga, A. Fasana, S. Marchesiello, L. Garibaldi, The politecnico di torino rolling bearing test rig: Description and analysis of open access data, Mech. Syst. Signal Process. 120 (2019) 252–273.
- the electrical locomotive rolling bearing dataset-.H. Wu, H.K. Jiang, S.W. Liu, et al., A deep reinforcement transfer convolutional neural network for rolling bearing fault diagnosis, ISA Trans (2022).
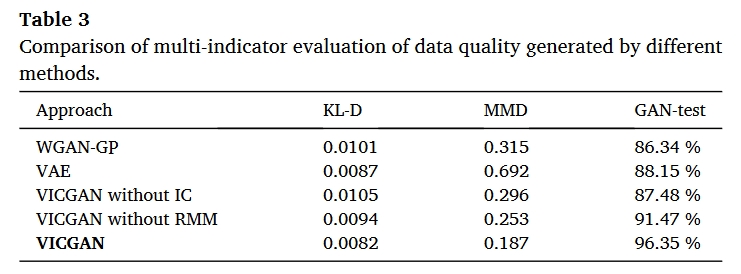
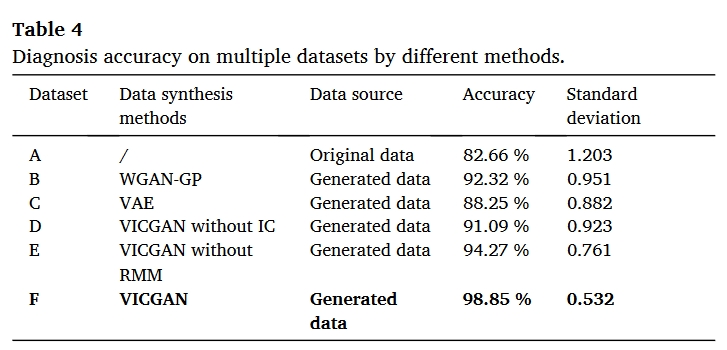
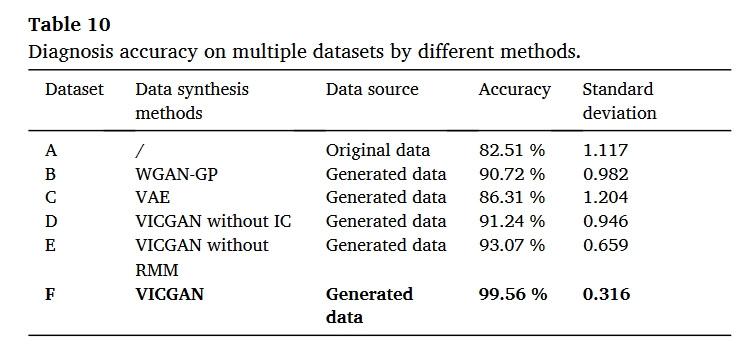
对比方法
- WGAN-GP
- VAE
- VICGAN without IC
- VICGAN without RMM
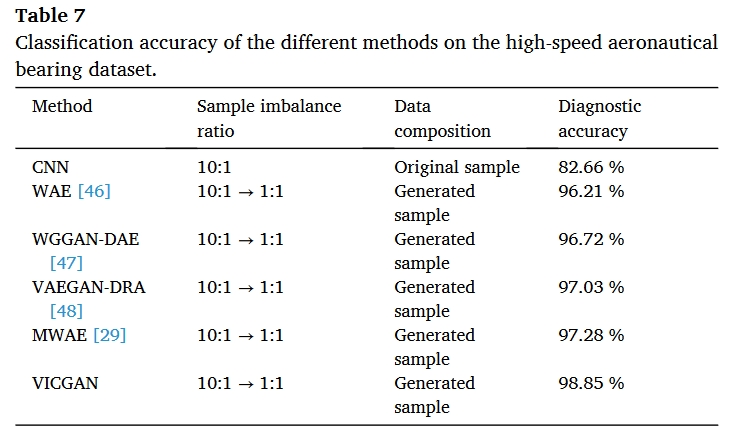
- CNN-WAE-2020-TIP
- WGGAN-DAE-2019-Meas. Sci. Tec
- VAEGAN-DRA-2021-Measrement
- MWAE-2019-KBS
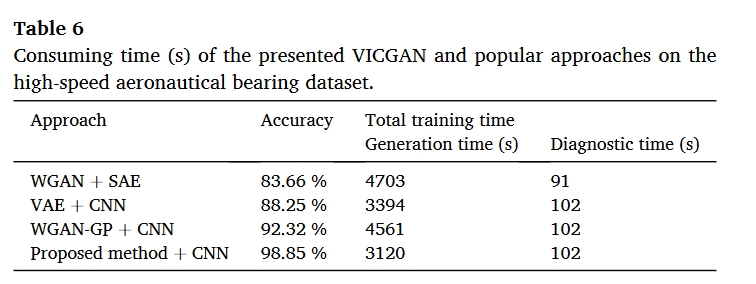
实验结果
总结
本文的创新点主要有三个
- 将自编码器加入生成器
- 利用形成瓶颈法提出了一种利用形成瓶颈法,以提高生成对抗结构的训练稳定性。
- 在网络中加入表征匹配模块以解决模式崩溃问题。
并且还和经典的WGAN+GP进行了对比,方法创新性还是比较高。小样本中实验中使用的是10个样本来进行生成。