引言

1. 滚动轴承是机械设备的基本部件，容易受到过载、疲劳、磨损和点蚀等因素的影响而损坏。故障会导致设备振动、停机或其他不可预测的损失，甚至造成人员伤亡。因此，对于滚动轴承来说，及时可靠的状态监测尤为重要，以确保安全可靠运行并降低维护成本。
2. 由于机械设备内部结构复杂、动态响应多样，正常信号和故障信号相互叠加、调制，仅仅采集或处理单一传感器的振动信号已经无法满足实际复杂系统的诊断要求。随着工业互联网的快速发展，大量传感器被用于机器状态监测。研究表明，多传感器信息融合技术可以提高故障诊断的效果。在现有研究中，多传感器信息融合在故障诊断领域的应用相对较少，且研究主要集中在数据级融合。然而，信息融合是一个多层次、多方面的过程。每个层次都是对原始观测数据的不同程度的抽象。因此，在故障诊断过程中，需要开发高效的融合规则和融合方法，实现多层级信号融合，以获取丰富的故障特征。
3. 介绍了数据驱动的故障诊断方法。从人工神经网络到深度学习、再到残差网络。此外，通过堆叠的深度网络结构仅提取单尺度特征，所获得的语义信息不足。因此，如何设计一个熟练的网络结构来平衡训练时间和故障诊断效果是研究的难点。
4. 该文提出了一种多传感器喝多尺度的模型。其主要包含三个部分：
   1. 构造相关峰度加权融合规则，实现三方向传感振动信号的融合。
   2. 多传感器融合结果将以二维矩阵的形式作为后续深度网络的输入。
   3. 基于深度多尺度残差网络，可以自适应地提取不同层次的深度特征。最后，特征融合确保了更丰富的故障信息被编译，以进一步提高故障诊断的准确性。
5. 总体而言，本文的主要创新点可以概括如下：
   1. 构建了一种新的2MNet框架，该框架可以有效地融合多个传感器信号，自适应地提取多尺度特征，从而提高滚动轴承故障诊断的准确性。
   2. 通过定义相关峰度加权融合规则，提出了多传感器融合概念，可以更全面地实现不同方向振动信号的融合，有效抑制噪声分量。
   3. 通过优化常规深度残差网络并添加扩张卷积，提出了一种多尺度特征提取方法，并结合金字塔原理实现了多尺度特征融合。对特征信息进行了重用和融合，丰富了故障信息的表达。

提出的2MNet

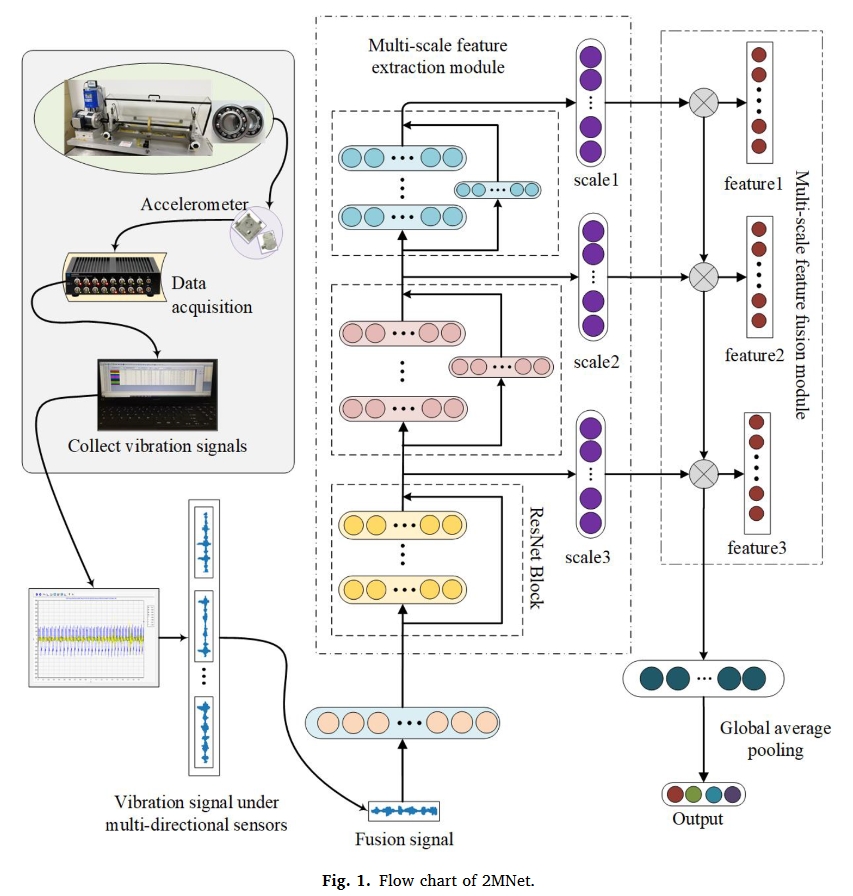
整体结构

如图1所示，2MNet主要包括三个部分：

1. 数据采集与处理：在数据采集和处理中，X、Y和Z三个方向的振动信号由加速度传感器采集。
2. 特征提取与融合：然后，利用所提出的融合规则对多传感器振动信号进行融合。。
3. 故障分类：融合后的信号被归一化并以二维矩阵的形式输入到2MNet中。

该网络包括输入层、深度残差卷积、多尺度特征提取和融合模块、全局平均池化层和分类。

特征可以通过多个卷积层自适应地表达，具有对移动、缩放和失真不变的特性，从而在一定程度上避免了对手动特征提取和选择的依赖。

传统的全连通层被全局平均池化层所取代，使得不同特征图之间的关系更加直观，并且可以很容易地转换为分类概率。

基于Adam梯度下降算法，加速了模型训练，提高了模型的可推广性。

此外，通过巧妙的网络结构提取和融合不同尺度的特征。最后，使用softmax作为输出层来实现故障分类。

多传感器信号融合

相关峰度加权融合规则的构建

在振动信号分析和特征提取的各种指标中，峰度[22]和相关系数[23]是两个被广泛使用的重要指标。

当轴承的工作面发生故障时，每转一圈都会产生冲击脉冲。在缺陷早期，故障越严重，冲击响应幅度越大，故障现象越明显。

峰度可以很好地反映振动信号的冲击特性，但仅取决于分布密度。因此，一些振幅较大但分布分散的冲击分量可以忽略不计。相关性表示统计学中的相关性程度。它可以用来表征信号之间的相似程度。相应地，信号能量值与相关度成比例，但易受噪声影响。因此，考虑到这两个指标的特点，构建了一种基于相关峰度加权的多传感器信号融合规则。

假设$x_1(n)、x_2(n),…,x_k(n)$是由k个传感器收集的信号，传感器i和传感器j之间的互相关表示如下:

$R_{i,j}=\frac1{N-m}\sum_{n=1}^{N-m}x_i(n)x_j(n+m)$

其中，N表示振动信号的总数，n表示信号长度，m表示互相关计算期间不同通道的离散信号的时间坐标移动值。因为来自多个传感器的信号同时被收集，并且波在固体中传播得非常快。因此，为了简单起见，这里的m被标记为0。

传感器i和传感器j收集的信号之间的互相关能量表示如下：

$E_{i,j}=\sum_{n=1}^N\left[R_{i,j}(n)\right]^2$

传感器i和其他传感器收集的传感器之间的总互相关能量计算如下：

$E_i=\sqrt{\sum_{\frac{j=1,}{j\neq i}}^k{E_{i,j}}^2}$

峰度指数的计算方法如下：

$K_i=\frac{\frac1N\sum_{n=1}^N\left[x_i(n)-\mu\right]^4}{\left(\frac1N\sum_{n=1}^N\left[x_i(n)-\mu\right]^2\right)^2}$

其中，μ 代表信号的平均值。

相关峰度加权融合规则的构造如下：

$W_i=\frac{E_iK_i}{\sum_{i=1}^kE_iK_i}$

因此，融合信号 Y 的表达式为：
$Y=\sum_{i=1}^kW_i\cdotp x_i(n)$

多尺度特征管道

在一般的故障诊断网络中，通常通过一系列卷积层和池化层提取特征，输出单尺度特征图进行分类识别。在精密机械系统中，故障振动信号较为复杂，单一尺度上的动态特征无法保证故障特征信息的完整性，因此需要考虑不同尺度信号的复杂性和随机性。

本文中的多尺度包括两个方面：

1. 通过多分支扩张卷积块提取改进残差网络的不同特征
2. 通过金字塔原理融合深层特征和浅层特征。

本节将分别介绍改进残差网络模块、多尺度特征提取和融合模块。

深度残差网络模块

多尺度特征提取与融合模块

多尺度特征提取是对不同粒度的信号进行采样，观察不同尺度的特征。一般来说，较小或密集的样本可以提供更多细节。相反，更大或更稀疏的样本可以得到总体趋势[25，26]。在本文中，通过空洞卷积来提取多尺度特征。在这个卷积过程中，不同尺度的局部特征被映射到不同的维空间，从而可以获得更丰富的故障信息。空洞卷积[27]是指在传统卷积的基础上增加零填充以扩展卷积核的感受野的卷积。与传统卷积不同，空洞卷积引入了一个称为“空洞率”的超参数，定义了数据处理过程中卷积核之间的距离。当卷积核的大小相同时，可以通过设置不同的扩张率来获得不同的感受野，从而获得多尺度信息。

空洞卷积主要表示如下：

实验

数据集

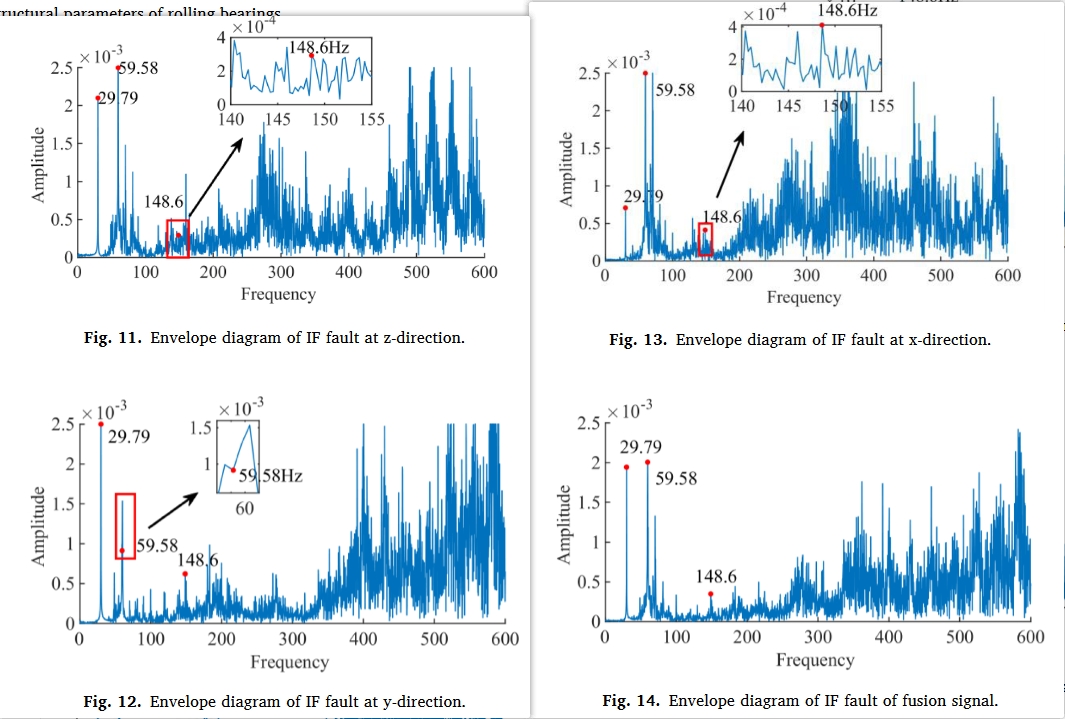
由于滚动轴承转速高，故障特征可能隐藏在高频信号中，并受到复杂的振动传递路径和严重的环境噪声干扰等因素的影响。信号中存在高频和低振幅分量，使得故障识别相对困难。因此在本文，构建了一个包含高频和低能量分量的模拟信号及其噪声信号，以验证信号融合的效果。

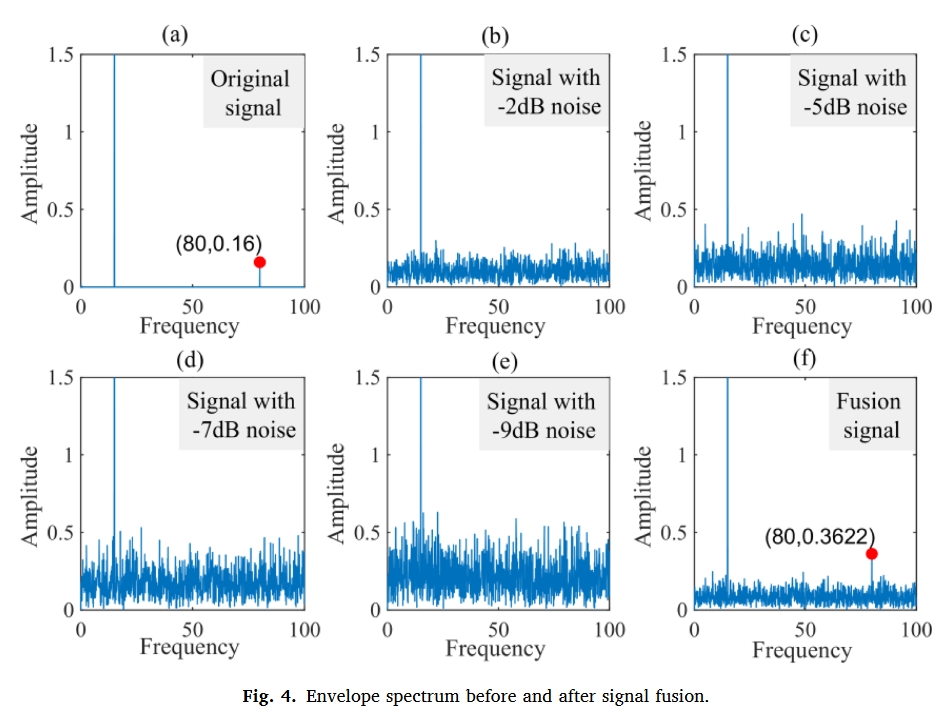
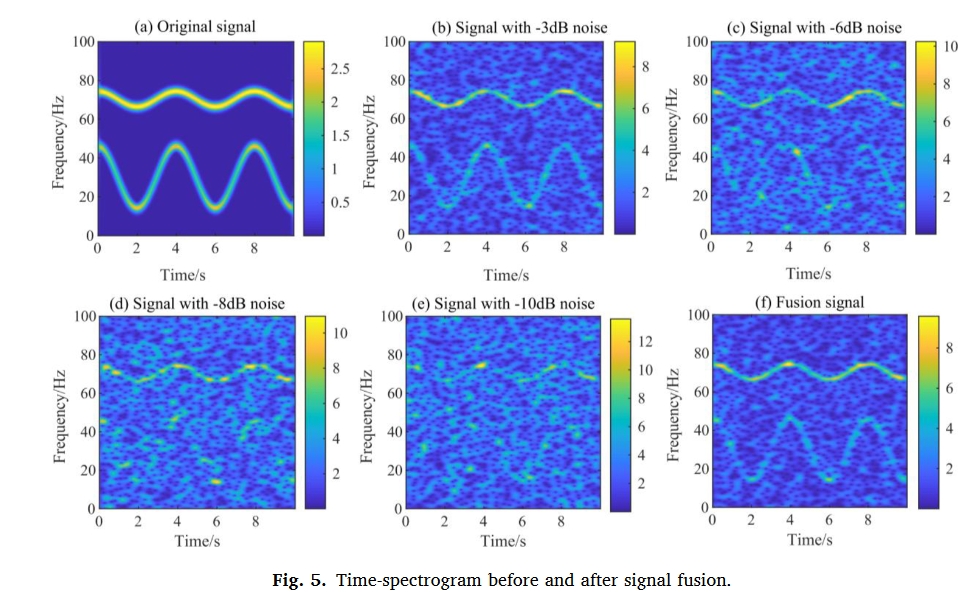
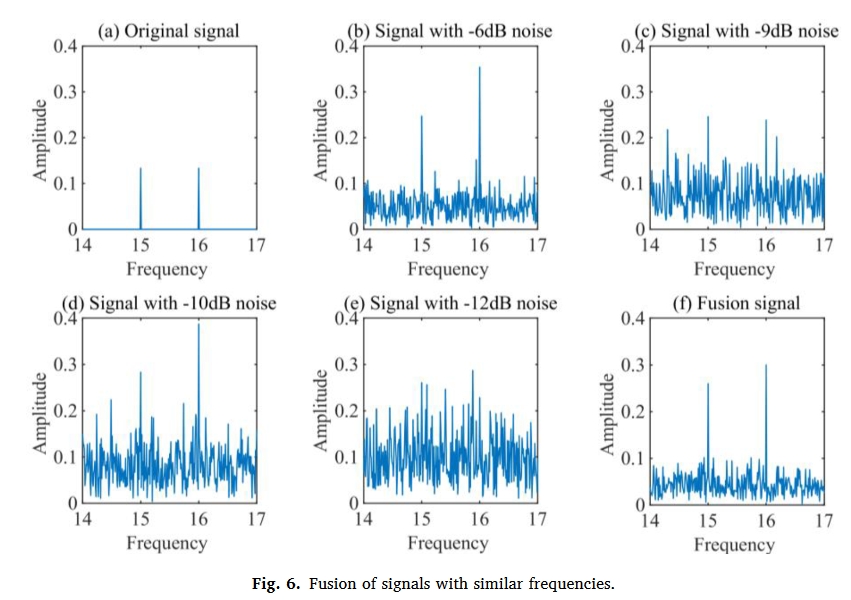
滚动轴承的振动信号大多是非平稳和非线性的。当振动状态发生变化时，采集到的信号可以显示出新的状态，便于在线监测和诊断。因此，本章采用来自燕山大学机械故障诊断台的滚动轴承数据集进行分析。

对比方法

1. VGG
2. ResNet
3. DCNN
4. Inception

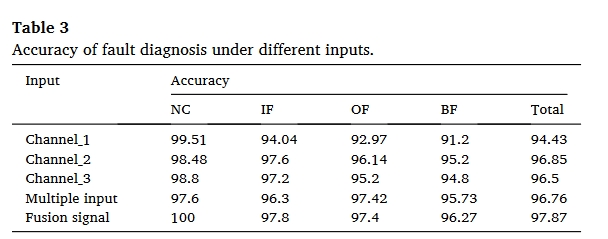
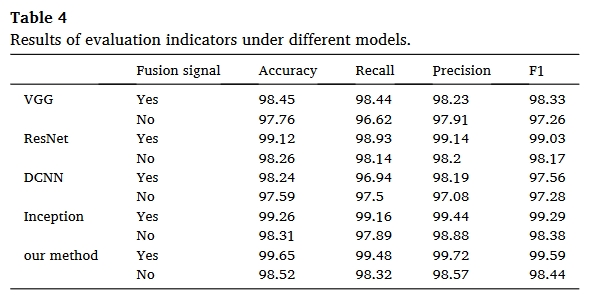
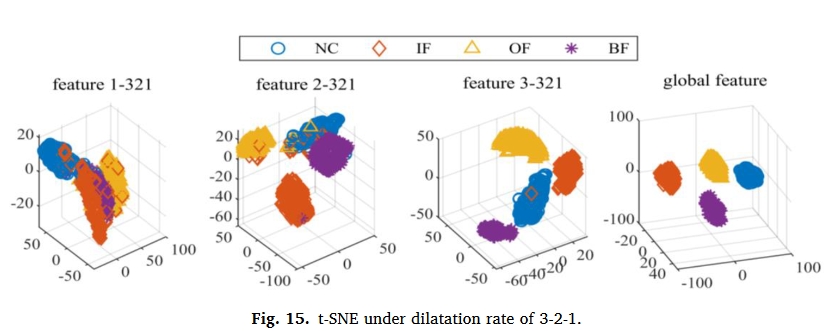
实验结果

总结

1. 本文的基于信号的统计量特征进行多信号融合很有启发性。
2. 提出的多尺度其实是比较normal的一种思路。