引言

1. 滚动部件使用广泛，且工作环境严峻，因此可能导致经济和人身安全。因此对其进行准确的诊断非常重要。

2. 介绍数据驱动故障诊断方法的三个主要步骤：

   1. 信号采集：通常测量诸如振动、温度、声学、电流等的各种信号。
   2. 特征提取和选择：提取并选择被认为对特定故障敏感的特征。
   3. 故障分类：在该步骤中，提取的特征用于训练基于机器学习的分类方法。

   然而，它们仍然有存在的缺点：

   1. 传统的基于机器学习的分类器在结构较浅的复杂分类任务中缺乏自动特征工程的功效。
   2. 研究人员为特定故障诊断问题精心设计的特征可能无法保证其在其他问题上的有效性。
   3. 由于很难确定表征特定故障的最佳特征，许多研究倾向于包括尽可能多的特征，以避免丢失敏感信息。

3. 介绍了深度学习，以及其在故障诊断领域中的一些工作。

4. 到目前为止，基于深度学习的故障诊断方法几乎所有的成功都是通过监督学习的框架实现的，这需要大量的标记数据。然而显示环境中很难获取大规模的标签。因此，开发一种能够在有限的标记数据集上获得有竞争力的结果的故障诊断方法具有现实意义。

5. 介绍半监督学习方法，其可以解决标签数据的缺少。其主要思想是：首先使用未标记的数据以无监督的方式对特征提取器进行预训练。然后，基于从标记数据中提取的特征，以有监督的方式训练分类器。

6. 一些半监督学习方法试图同时处理标记和未标记的数据。例如，条件变分自动编码器（VAE）[32]及其变体[33]通过引入用于编码类标签的额外潜在变量以及用于提高分类精度的显式分类损失来扩展无监督VAE，使得它们可以同时从标记数据和未标记数据中学习。因此，在本文中，我们提出了一种简化的半监督故障诊断方法，称为混合分类自动编码器（HCAE），该方法是通过将softmax分类器连接到自动编码器的中间隐藏层来开发的。总之，本文的主要贡献如下。

   1. 提出了一种新的旋转机械故障诊断半监督学习模型。通过修改架构和成本函数，该模型可以同时从标记和未标记的数据中学习。据我们所知，这是应用于故障诊断任务的开创性工作。
   2. 通过电机轴承数据集和工业水轮机数据集验证了所提出的方法。与现有的一些方法相比，该方法的性能有了显著的提高，尤其是在小标记数据集的情况下。这使得我们的方法在实际工业应用中更加实用。
   3. 为了解释该方法的有效性，Grad-CAM[34]被应用于定位输入中对网络预测贡献最大的区域。通过这样直观的解释，我们可以更好地理解所提出的模型的诊断原理。

相关工作

自编码器

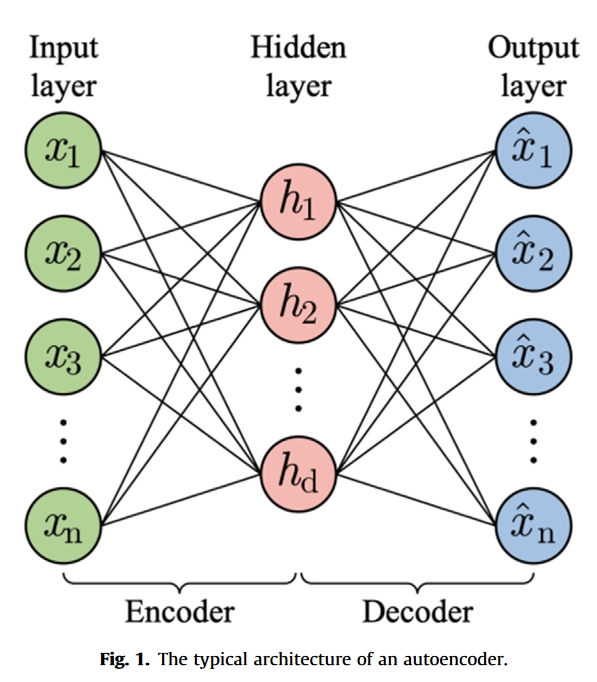
softmax 回归

Hybrid classification autoencoder for fault diagnosis

本节详细介绍了用于旋转机械故障诊断的HCAE。该方法如图2所示。

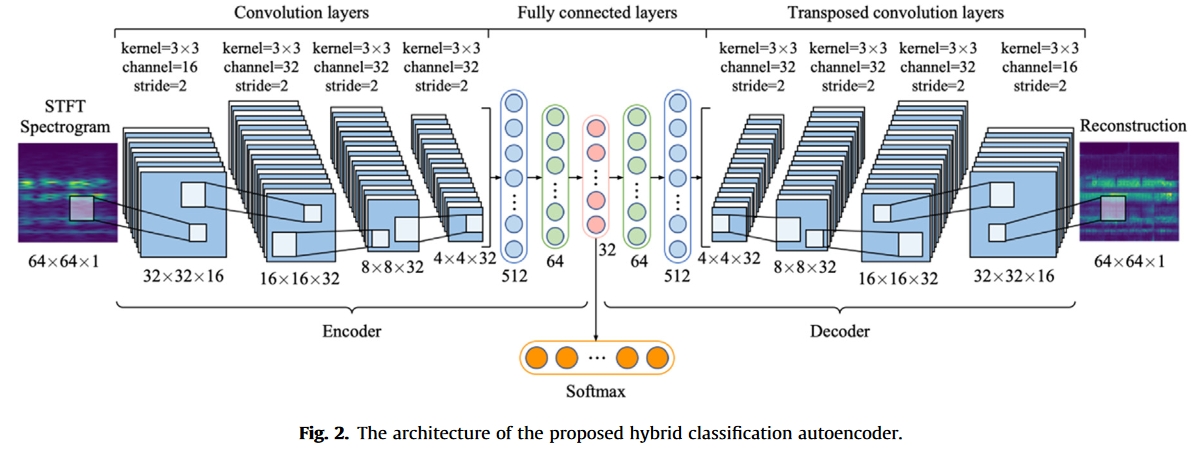
该方法如图2所示。如图所示，该模型被设计为一输入两输出配置。一个输出是从深度卷积自动编码器获得的输入时频图像的重建。另一种是基于编码特征的softmax分类器输出的健康状况预测。

数据预处理

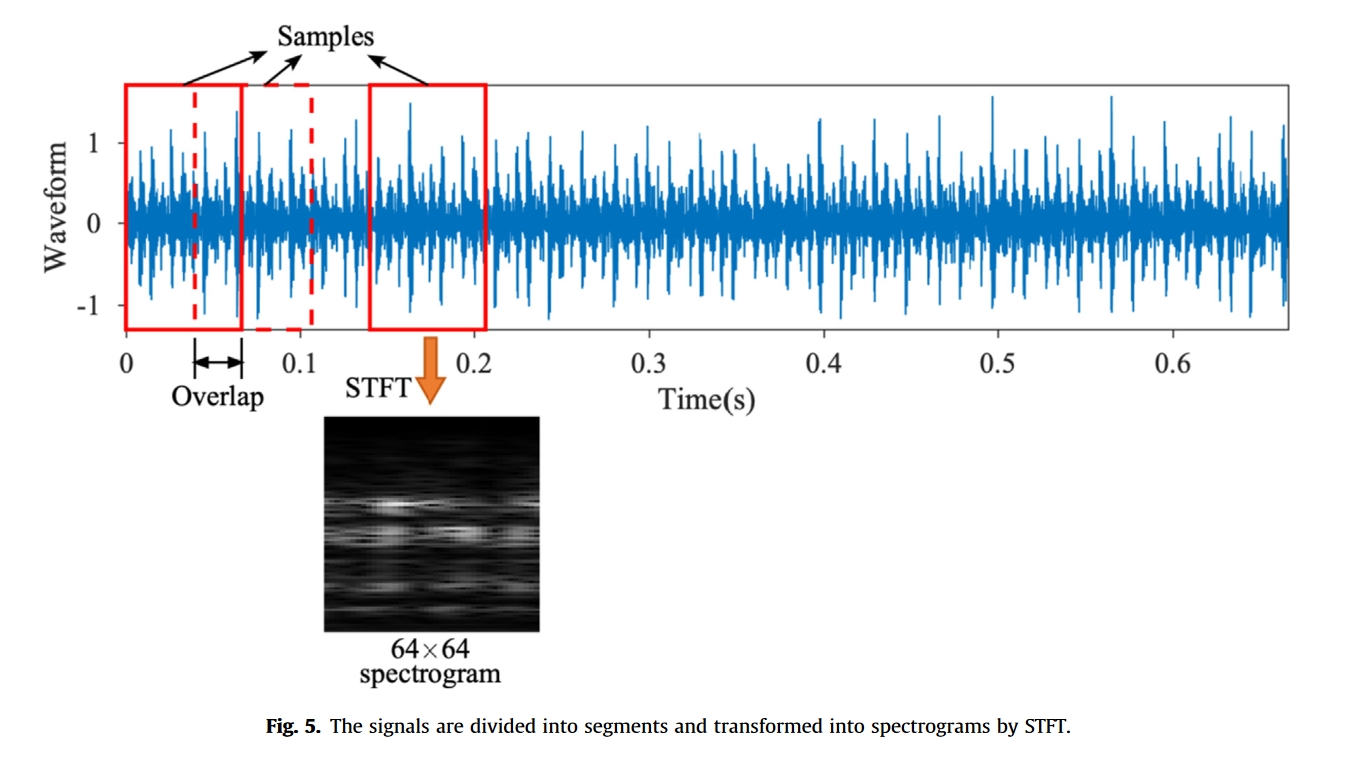
短时傅立叶变换（STFT）谱图被用作所提出的模型的2D输入。采用频谱图作为输入的优点是，由于振动信号在故障条件下通常表现出非平稳行为，因此频谱图是其在时域和频域中定位动态特征的能力的代表性输入。此外，与需要手动选择的小波来适应信号中的特征的小波变换相比，STFT是一种简单易用的信号处理方法，需要很少的先验知识。

通常，数据预处理包括三个步骤：

1. 首先通过STFT将时间序列振动信号$x(t)$转换为2D频谱图$X(\tau, ω)$:

   $$X(\tau,\omega)=\int_{-\infty}^{+\infty}x(t)w(t-\tau)e^{-j\omega t}dt$$

2. 频谱图本质上是一个复矩阵，表示信号在时间和频率上的幅度和相位。为了方便后续数据处理，将谱图转换为由0到1的归一化幅度组成的灰度图像。这可以按以下方式进行:

   $$X^*(\tau,\omega)=\frac{|X(\tau,\omega)|-|X(\tau,\omega)|{min}}{|X(\tau,\omega)|{max}-|X(\tau,\omega)|_{min}}$$

   其中$X(\tau, ω)$计算谱图的元素谱图，并且$|X(\tau, ω)|{max}$和$|X(\tau, ω)|{min}$分别$X(\tau, ω)$是谱图中的最大和最小幅度。

3. 最后，将归一化频谱图压缩为$64\times64$时频图像，以降低计算成本并便于模型的训练。

数据编码

数据解码

故障诊断

上面的编码器-解码器架构并不是什么新鲜事，只是一个堆叠的卷积自动编码器。HCAE中的独特设计是直接连接到中间隐藏层的softmax回归。通过这个额外的输出通道，可以通过使用等式来诊断健康状况。（5）基于来自编码器的编码特征。

Semi-supervised learning of HCAE

在训练过程中，采用梯度下降法对HCAE的可学习参数进行优化。由于HCAE的多个输出，训练这样的模型需要为网络的不同输出指定不同损失函数的能力。在我们的特定模型中，我们使用二进制交叉熵损失来评估卷积自动编码器的重建误差，并使用分类交叉熵损失测量softmax预测和标记数据的真实标签之间的距离。因此，为了为梯度下降训练算法建立一个独特的目标，将这两个损失组合成一个单独的成本函数，如下所示：

$$f(\mathbf{W}{en},\mathbf{b}{en},\mathbf{W}{de},\mathbf{b}{de},\theta)=\int_{BC}(\mathbf{W}{en},\mathbf{b}{en},\mathbf{W}{de},\mathbf{b}{de})+\alpha\cdot J_{CE}(\mathbf{W}{en},\mathbf{b}{en},\theta)$$

其中，$W_{en}$和$b_{en}$分别是编码器的权重矩阵和偏置向量。$W_{de}$和$b_{de}$是解码器的权重矩阵和偏置向量。a是控制卷积自动编码器的无监督学习和softmax回归的有监督学习之间的相对权重的系数。作为模型中的一个超参数，a的最优值可以通过机器学习和系统识别社区广泛采用的交叉验证方法有效地确定。应该注意的是，在JCE中仅应用标记数据来微调权重矩阵Wen、编码器的偏置向量$b_{en}$和softmax分类器的权重h。

利用组合成本函数，可以以无监督的方式训练HCAE中的卷积自动编码器进行特征提取，同时以有监督的方式培训HCAE的softmax分类器进行故障诊断。换句话说，所提出的HCAE可以随时从标记和未标记的数据中学习。与传统的半监督学习方法（试图在两阶段学习方案中独立地从未标记和标记的数据中学习）相比，该方法有望以更自然、更通用的方式学习，以获得故障诊断能力。

实验

数据集

1. Case Western Reserve University

实验结果-CWRU

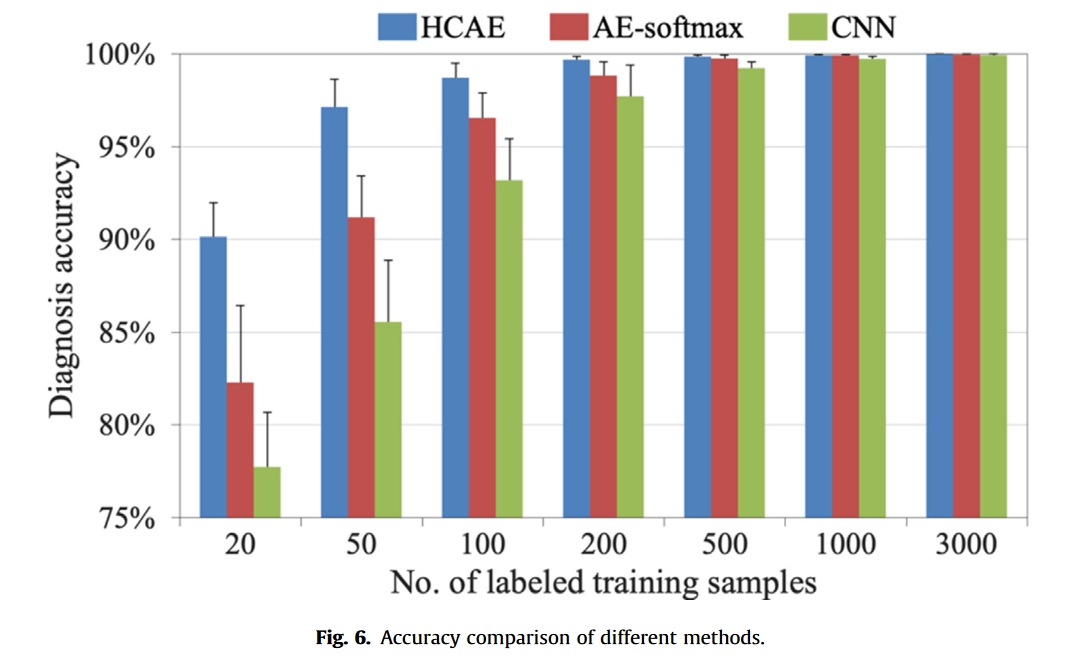
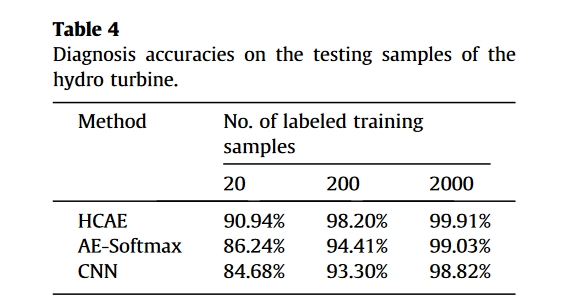
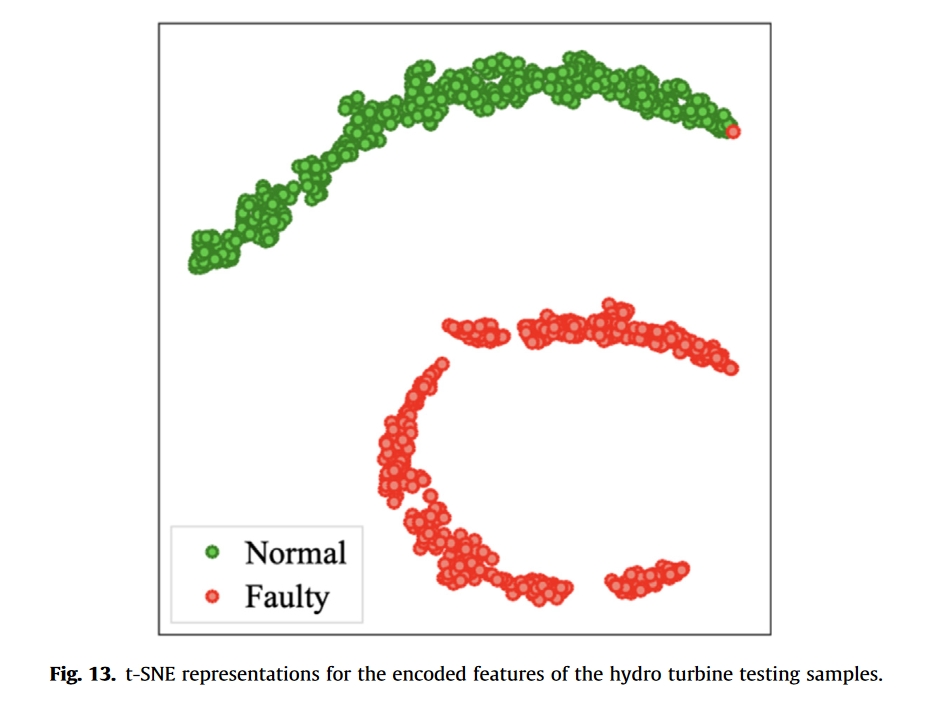
实验结果-工业应用：水轮发电机转子的故障诊断

总结

本文提出了一种半监督的自编码器，但是创新性不算很高。