期刊: Engineering Applications of Artificial Intelligence(IF:8)
引言
滚动轴承很重要,对其进行诊断非常关键。
介绍深度学习技术以及在故障诊断领域中的应用。
介绍网络压缩的相关知识,文献分析揭示,基于深度神经网络的诊断方法通常通过构建复杂结构、深化网络来提高性能,但这导致大量参数、高硬件需求、训练时间长。研究指出,多层神经网络存在冗余参数,对性能影响小,因此提出通过压缩深度网络、消除冗余参数,平衡精度和设备需求,以适应资源受限的实际工业环境,提高在线监测和诊断性能。
压缩深度神经网络的主要目的是压缩效果显著但参数数量巨大的网络。网络修剪是一种广泛使用的网络压缩方法,它可以同时修剪卷积(Conv)层和全连接(FC)层。修剪方法进一步分为结构化修剪和非结构化修剪:
- 结构化修剪:通过压缩Conv层实现网络加速。
- 非结构化修剪:减少网络参数所占用的内存,通过将参数修剪到阈值之下。
分别介绍了一些结构化和非结构化剪枝的方法。
仅依赖结构化和非结构化方法不够。且目前故障诊断的方法大都基于深度和庞大的网络这导致利用这些模型实现实时智能在线故障诊断很困难。
针对上述问题,本文提出了一种将结构化和非结构化修剪、量化和矩阵压缩相结合的多层次压缩方法。它可以同时压缩网络的Conv层和FC层,并对其参数进行量化,最后通过矩阵压缩进一步减少了参数所需的存储空间。本文的主要贡献总结如下:
- 提出了一种多层次网络压缩方法,并将其应用于基于DNN的轴承故障诊断,旨在从多个角度大幅减少参数量和浮点运算。
- 引入了一种复合修剪过程来同时压缩卷积层和全连接层,这减少了参数的数量,加快了训练和响应。
- 将参数量化与矩阵压缩相结合,进一步压缩了模型,并降低了部署在监测设备中的存储和计算需求。
提出的方法
方法的主要思想:
- 在结构化修剪阶段消除Conv层中的无关紧要的滤波器,以减少网络中的FLOP,加速网络训练,然后在修剪后对网络进行微调,以恢复其性能;
- 通过非结构化修剪去除FC层中不重要的连接,从而减少了参数的数量;最后,对剩余的参数进行量化,并通过聚类和权重共享来减少表示权重参数的比特数。
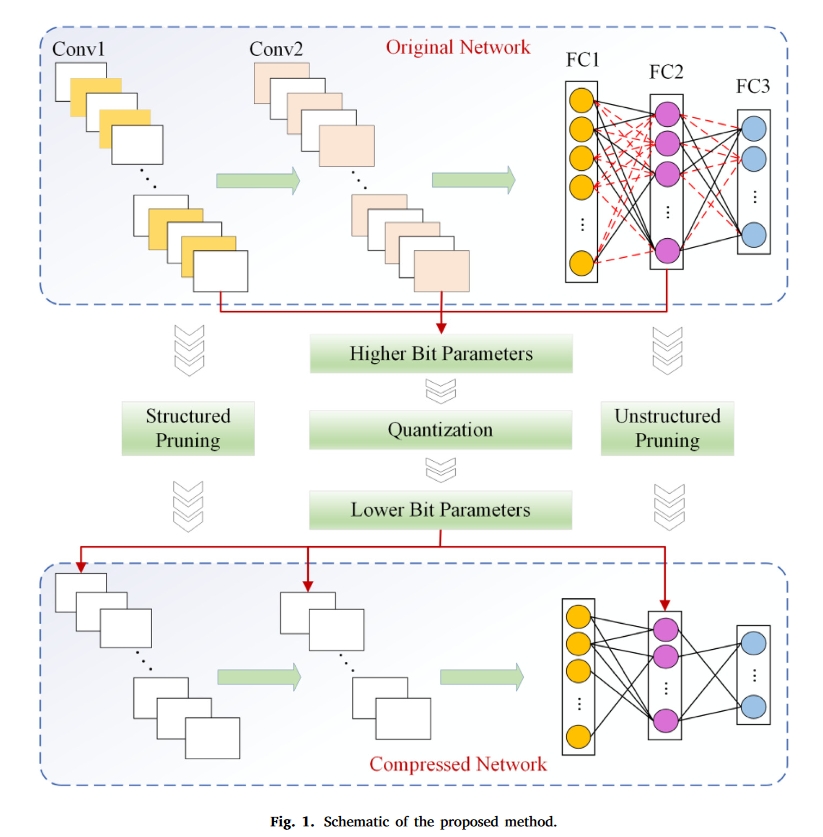
结构化剪枝
基于CNN的深度神经网络的主机通常由多个Conv层和FC层堆叠而成。滤波器在每个Conv层中的卷积运算通常会产生大量的参数和FLOP,冗余滤波器产生的结果也包括在内。因此,去除这样的滤波器可以节省存储空间和计算能力,而不会影响模型性能。作为滤波器和输入数据的卷积输出,特征图指示了特征的不同重要性。本文提出通过计算每个卷积核的特征图的输出秩来衡量卷积结果的重要性;然后去除与特征图的低秩输出相对应的滤波器,从而实现网络压缩和加速。
非结构化修剪
网络模型的参数主要集中在全连接层。非结构化剪枝可用于剪除 FC 层中的冗余连接,从而减少网络参数的数量。对网络中每个 FC 层的参数进行排序,将低于某个阈值的参数定义为冗余参数。删除这些参数不会明显影响网络精度,但会降低所需的参数存储容量。
参数量化
参数量化旨在最小化表示每个权重所需的位数,以实现网络压缩。
主要有两种方法,即权重共享和低位表示。本文采用层内(层与层之间不共享)权重共享的方法实现权重量化。通过对各层的权重矩阵应用 k-means 聚类算法得到聚类中心和相应的聚类指数,每个权重用其所在的聚类中心代替,最后只需存储其聚类中心和聚类指数。权重共享聚类过程如图 3 所示,其中相同颜色表示聚类为一类。
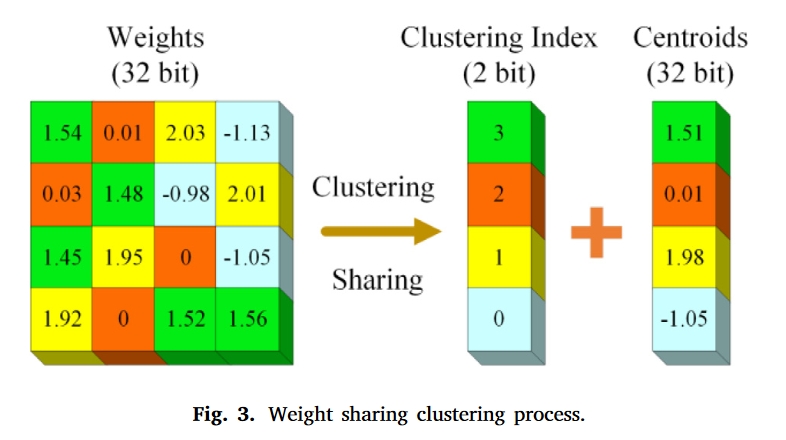
量化后的权重从原来的32位浮点表示为2位聚类索引和32位聚类中心,这使得存储的数据量大大减少。如果群集类别为𝑘, 索引数为log2(𝑘) 位,并且在具有𝑛 权重,如果每个权重由𝑏 位,压缩率𝑅 可以表示如下。
$R=\frac{nb}{nlog(k)+kb}$
在图3中,原始权重矩阵大小为4×4,即权重个数为16,聚类类别为4,每个权重用32位表示,得到压缩率为16×32∕(16×2+4×2)=3.2。
权重矩阵压缩
通常,高阶权重矩阵中存在许多具有相同值的元素,它们可以在稀疏后通过矩阵压缩进行存储,以进一步节省存储空间。目前稀疏矩阵的压缩存储方法主要包括压缩稀疏行(CSR)和压缩稀疏列(CSC)。本文采用CSR,处理如下:如果稀疏矩阵的非零值远小于零元素,则每个非零元素只存储三项,即元素值、行索引和列索引。Let矩阵𝐴 4矩阵,𝑎𝑖𝑗 是𝑖第行和𝑗中的第th列元素𝐴, 𝑖, 𝑗 ∈ {1,2,3,4},其中𝑎12,𝑎21,𝑎22,𝑎33,𝑎42不为零,其余元素为零,矩阵由CSR存储。
并非所有索引矩阵在量化的聚集索引矩阵中都是稀疏的。因此,本文对这些索引矩阵进行稀疏处理,将这些具有相同值和最大数的元素设置为零,然后使用矩阵压缩方法来存储聚集的索引矩阵。让索引矩阵的每个元素𝐴 是𝑎𝑖𝑗 , 以及索引的数量𝑘 是𝑛𝑘, 稀疏的𝑎𝑖𝑗 表示如下。
$a_{ij}^{‘}=a_{ij}-max{n_i}$
至此,上述过程完成了对整个网络的压缩。
实验
数据集
- XJTU-SY rolling bearings dataset
- CWRU bearing dataset
结果
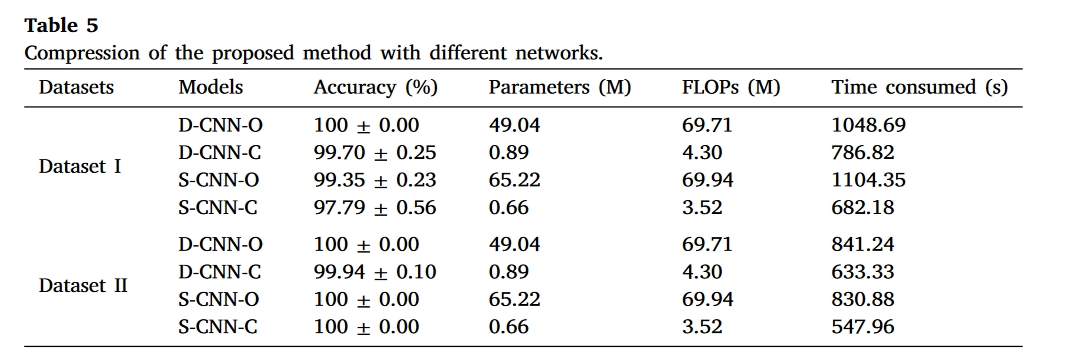
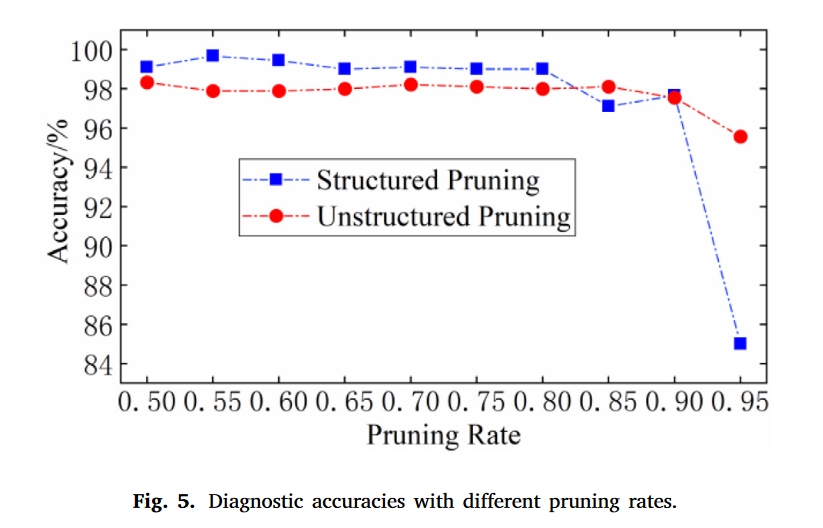
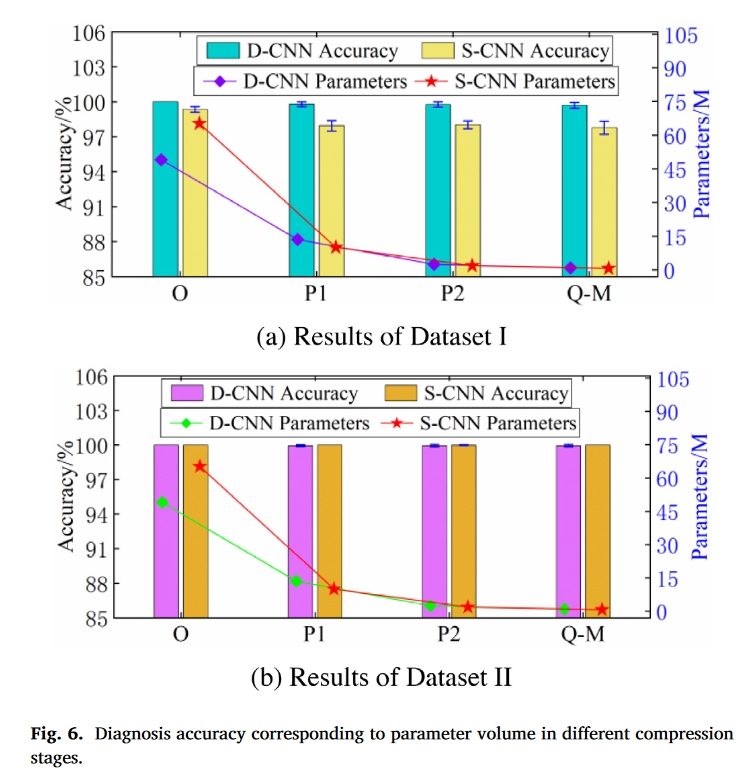
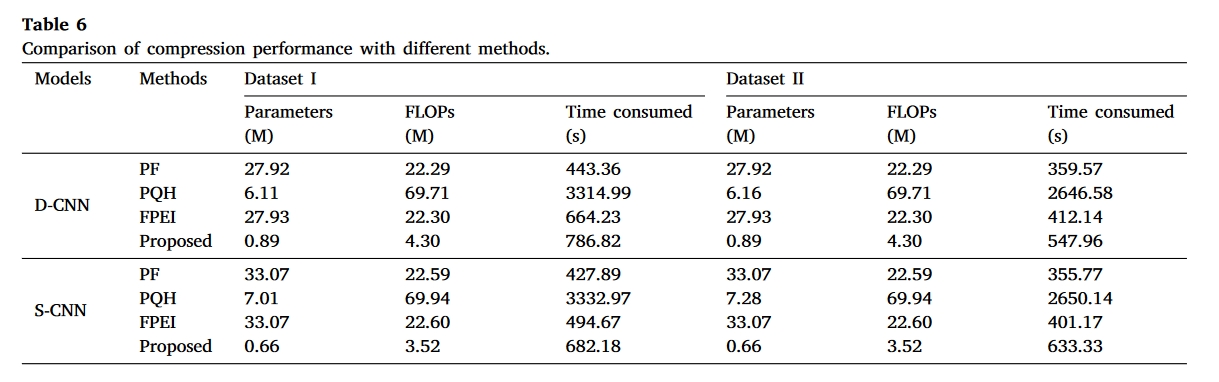
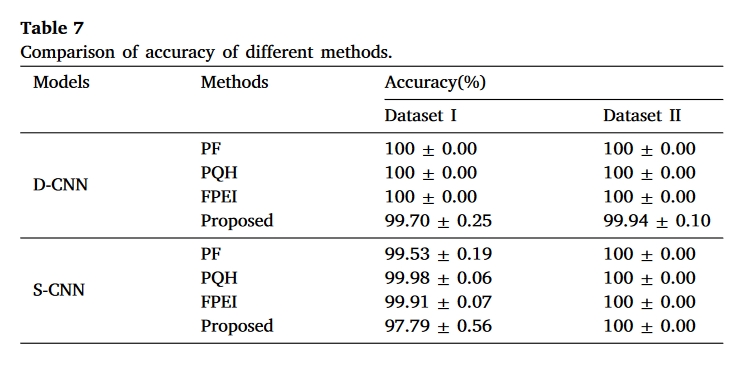
总结
通过这篇论文了解了网络压缩也可以用在故障诊断这个领域中。但是本文的创新有限,方法论上面都是常见的方法的组合。