引言

1. 在旋转机械和设备中，滚动轴承是一个重要的支撑部件。防止滚动轴承运行状态异常对旋转机械造成不可修复的损坏的最简单方法是及早发现问题并区分故障类型。设备故障检测和诊断是一个非常具有挑战性的问题。研究人员提出了多种方法来解决设备故障诊断问题，包括：

   1. 时间频率分析
   2. 基于模糊的控制
   3. 稀疏信号分解

   数据驱动的智能故障检测方法可以从采集的设备运行数据中获得知识。到目前为止，研究人员已经提出了各种基于深度学习（DL）的智能缺陷诊断模型。

2. 传统DL方法效果很好。不幸的是，为了训练基于DL的故障诊断模型，需要来自目标设备的大量标记数据。例如，当设备的转速和负载发生变化时，收集到的数据的特征分布将偏离先前状态的特征分布。在实践中可能会出现的大量标记数据通常来源于在各种环境中进行操作时收集的数据。因此，研究人员开发了基于迁移学习（TL）的智能故障诊断。

3. 介绍了迁移学习相关知识。比如Maximum Mean Discrepancy (MMD)为基础的CNN方法。

4. 滚动轴承通常在复杂的条件下工作，例如速度和负载的变化。尽管上述基于迁移学习的智能缺陷检测方法具有较高的检测能力，但在利用MMD进行测量学习时，找到合适的映射核函数是至关重要的。此外，在高维空间中进行测量将延长模型的计算时间。为了解决上述问题，本研究提供了一种基于中心矩差异（Central Moment Discrepancy, CMD）的TL故障诊断技术：基于局部CMD（LCMD）的滚动轴承多尺度CNN（MS-CNN）偏移故障检测。以下是本文的主要贡献：

   1. 基于MS-CNN-LCMD的方法提取了可以更有效地在Ds和Dt之间传输的信息。
   2. 所提出的技术通过避免大量内核参数选择的需要，更多地利用了跨多个领域的迁移学习。
   3. LCMD在跨领域诊断中的表现优于经典的CMD度量学习。(?)

相关工作

类子空间域对齐问题的描述

假设有两个数据集：

1. 源域：$D^s={x^s_i,y^s_i}^n_{i=1}$
2. 目标域：$D^t={x^t_j,y^t_j}^m_{j=1}$

然而目标域的标签$y^t_j$往往不能获取，因此往往使用伪标签来进行处理。

因此本文主要基于3个假设：

1. $D_s$中的标签数据足以完成模型的训练。在实验中，$D_s$包含了足够多的标记轴承运行数据。数据是在一定的运行条件下从轴承中收集的。
2. $D_t$不能获得大量的标记数据，只能获得有限的标记数据而不能完成模型的训练。$D_t$的数据是在与$D_s$不同的操作条件下从轴承中收集的。
3. 在负载调整和速度转换的情况下，子空间中的$D_s$和$D_t$具有相同的类别，$y^s$＝$y^t$。

基于CMD的DA故障检测

在DA问题中，通常使用MMD和Kullback-Leibler（KL）度量。基于KL发散的度量匹配可以与一阶矩匹配进行比较。原始矩的加权和可以用于近似基于MMD的度量匹配。

在数学和统计学中，矩用于测量变量分布的性质。在统计学中，第一矩与平均值相关，第二矩与方差相关，第三和第四矩与信号的偏度和峰度相关。信号的独特分布反映在中心距离上。假设X是一个随机变量。$X_k$的数学期望$E(X_k)$已知为随机变量X的k阶矩，如果$E(X_k)$存在。$[X-E(X)]^k$被称为X的k阶中心矩，如果它存在（k=1,2，…）。如果随机变量$X=(X_1，X_2，…，X_n)$和$Y=(Y_1，Y_2，…，Y_n)$在两个概率分布p和q上的区间$[a，b]^N$上独立且相同地分布。中心矩偏差可计算如下。

$$CMD(p,q)=\frac{1}{|b-a|}|E(X)-E(Y)|2+\sum{k=2}^{\infty}\frac{1}{|b-a|^k}|c_k(X)-c_k(Y)|_2$$

其中$E(.)$表示变量的数学期望，k表示阶数，$c_k(.)$代表变量X的中心矩。

$c_k(X)$的表达式如下:

$$\left.c_k(X)=\left(E\left(\prod_{i=1}^N\left(X_i-E(X_i)\right.\right)^{r_i}\right)\right)$$

其中$r_1 + r_2 + … + r_N = k$, 并且 $r_1, r_2,…,r_n ≥ 0$.

概率论/数理统计里，k阶矩实际上就是想表示k个「维度」下的move to average（移动到平均位置）这么件事儿，也就是把一列随机变量的(probability) mass之类的东西集中到一点，然后等效为「一个（k阶的）瞬间」，将所有的（一到无穷阶）「瞬间」集合到一起，可以完整描述这列随机变量。和物理里moving power的想法如出一辙，所以聪明的老人家用了moment（矩）这个词。

于是，不论是概率论/数理统计中，还是物理中的矩，在数学里可以被抽象成了同一类泛函)：

$\int x^k f(x) dx$。

具体而言：

零阶矩（概率）质量的总和。

一阶原点矩，即均值，也是大众理解的那个「平均」——衡量数据的平均水平。

二阶中心距，方差，衡量数据的离散/集中程度，也就是数据的「平均程度」。（这个表述不是很好，请大家脑补体会一下我的真实意思……）

二阶原点矩， $EX^2$ ，衡量数据被「移动至平均位置」需要的「平均能量」。相当于物理中的惯性矩。

三阶中心矩，偏度，衡量偏离中心的点的位置情况，也就是偏离中心的点的平均水平（正负、大小）。放到分布图像上看，就是均值和中位数之间的距离，也就是数据分布的对称性——对称分布偏度为零。

四阶中心矩，峰度，俗称「方差的方差」，衡量偏离中心的点的密集程度。是俗话说的「尖峰厚尾」的理论基础。

提出的MS-CNN-LCMD

LCMD的建立

朱[45]提出的基于LMMD的DSAN诊断方法影响了LCMD测量方法。作者在这个技术中提出了子域的概念。

现有$D_s$和$D_t$之间的环境将来自两个域的样本分离为一个公共子域。然后在子域中，对齐$D_s$和$D_t$的分布。在训练阶段，基于CMD的标准测量学习直接评估$D_s$和$D_t$数据之间的全局差异，并最大限度地减少两个领域数据集之间的损失。然而，当小批量中源域和目标域之间的数据类别分布存在显著差异时，直接计算两个域的全局偏差的方法可能会产生一些额外的偏差。在同一子域空间中，两个域之间的类别关联被忽略。

本文提出了一种基于LCMD的测量系统，以优化Ds和Dt之间的测量方式。当来自同一故障类别的信号传输到同一故障工作台时，它们显示出更大的关系。从源域数据$D_s$中收集大量标记数据通常很简单，而目标域$D_t$中只有少量标记数据。在计算两个域之间的距离时，使用$D_s$的标记数据和$D_t$的伪标记数据进行类别检测。创建了故障类型定义的局部空间，并在故障类型空间中执行源域和目标域的测量学习。因此，LCMD的定义如下：

$$LCMD(X,Y)=\sum_{c=1}^c(w^cCMD(X^c,Y^c))$$

其中，c是源字段和目标字段中的类别数，$w^c$表示批次中每个类别的百分比。以下是$w^c$的计算公式:

$$w^c=\frac{y^c}{\sum_{c=1}^Cy^c}$$

当映射函数为$f(.)$时，设$D_s$映射后的输出为$O^{sc}_z＝(O^{sc}_1，O^{sc}_2，…，O^{sc}_z)$，并且Dt映射后的输出为$O^{tc}_z＝(O^{tc}_1，O^{tc}_2，…，O^{tc}_z)$。子空间中基于类别的k阶局部偏差定义为：

$$l_{lcmd}=LCMD_K(O_z^s,O_z^c)=\sum_{z=1}^c(w^cCMD_K(O_z^c,O_z^c))$$

$CMD_k$可以如下计算:

$$w^cCMD_K\left(O_z^c,O_z^{tc}\right)=\frac{w^c}{|b-a|}|E\left(O_z^{sc}\right)-E\left(O_z^{\prime c}\right)|2+\sum{k=2}^K\frac{w^c}{|b-a|^k}|c_k\left(O_z^{sc}\right)-c_k\left(O_z^{\prime c}\right)|_2$$

MS-CNN

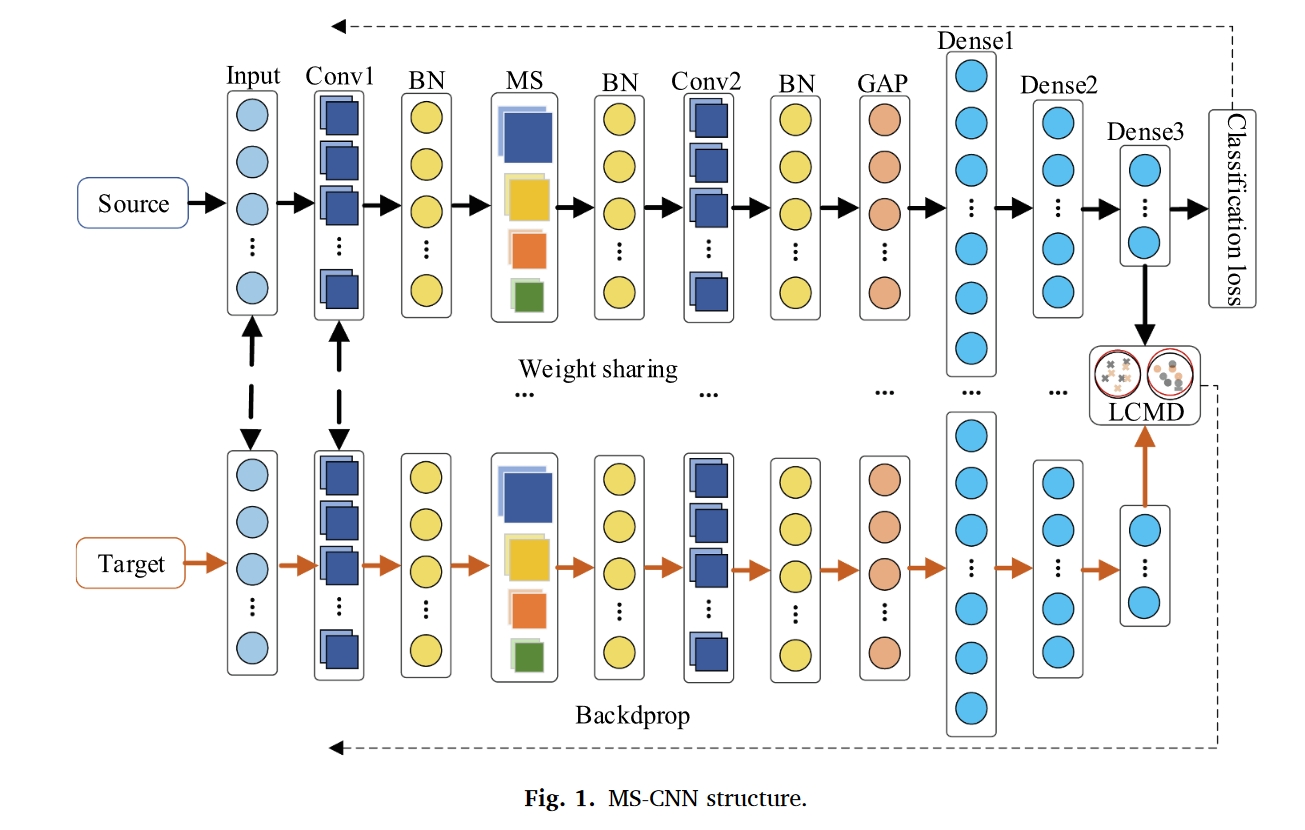
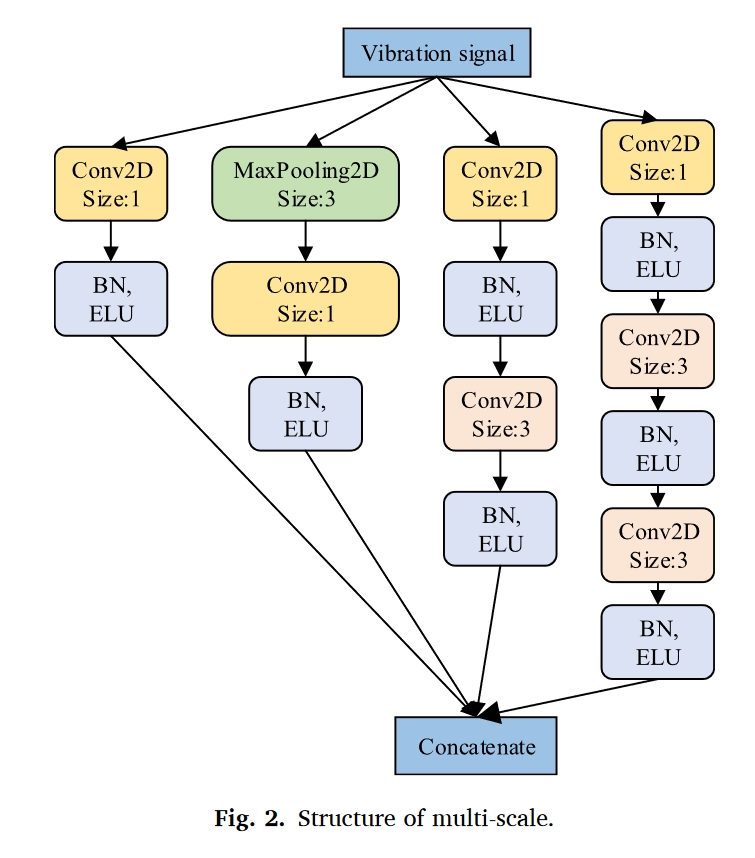
用ELU代替RELU激活函数，ELU具有更快的收敛速度和更高的精度，以防止多尺度特征提取和融合过程中的梯度消失，避免RELU神经元死亡[46]。最后，通过全连接层和softmax函数实现了特征提取和分类。ELU激活函数具有以下公式：

$$ELU(x)==\begin{cases}x&x\geqslant0\e^x-1&x<0&\end{cases}$$

训练方法

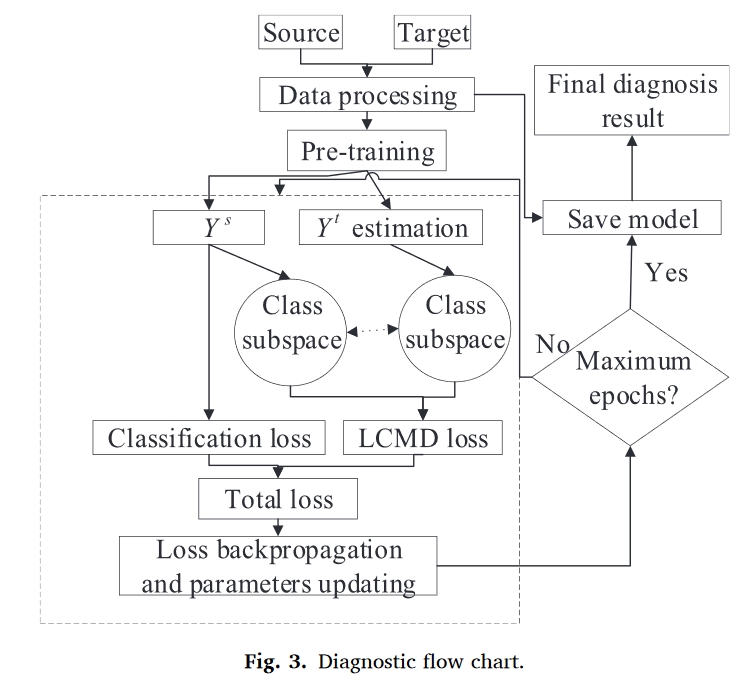
一旦收集并预处理了$D_s$和$D_t$数据，就使用现有的标记工况数据对模型进行预训练。如图3所示，当获取$D_s$数据和$D_t$数据时，对获取的数据进行处理。该过程包括数据归一化、截取和2D灰度转换。使用经过预处理的标记数据对模型进行预训练。当模型在源域上完成诊断任务$T_s$时，可以获取与目标域相关的故障知识。

然后，对来自$D_s$的数据和来自$D_t$的数据进行子空间映射，并在子空间中使用模型对$D_t$的伪标签和对$D_s$的实际标签，建立了一种基于类别空间中中心矩差的技术。在基于类的子空间中，两个域之间的分布差被最小化。最后，使用梯度反向传播来更新模型权重。并冻结最终模型的参数并保存模型。使用经过训练的模型来识别Dt。

实验

数据集

1. YSU bearing
2. CWRU experimental bearing

实验结果

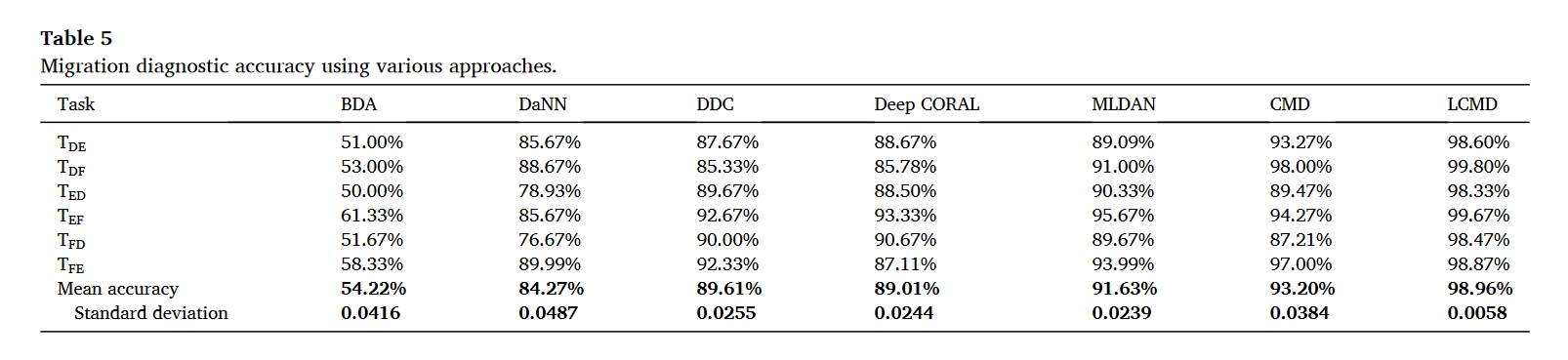
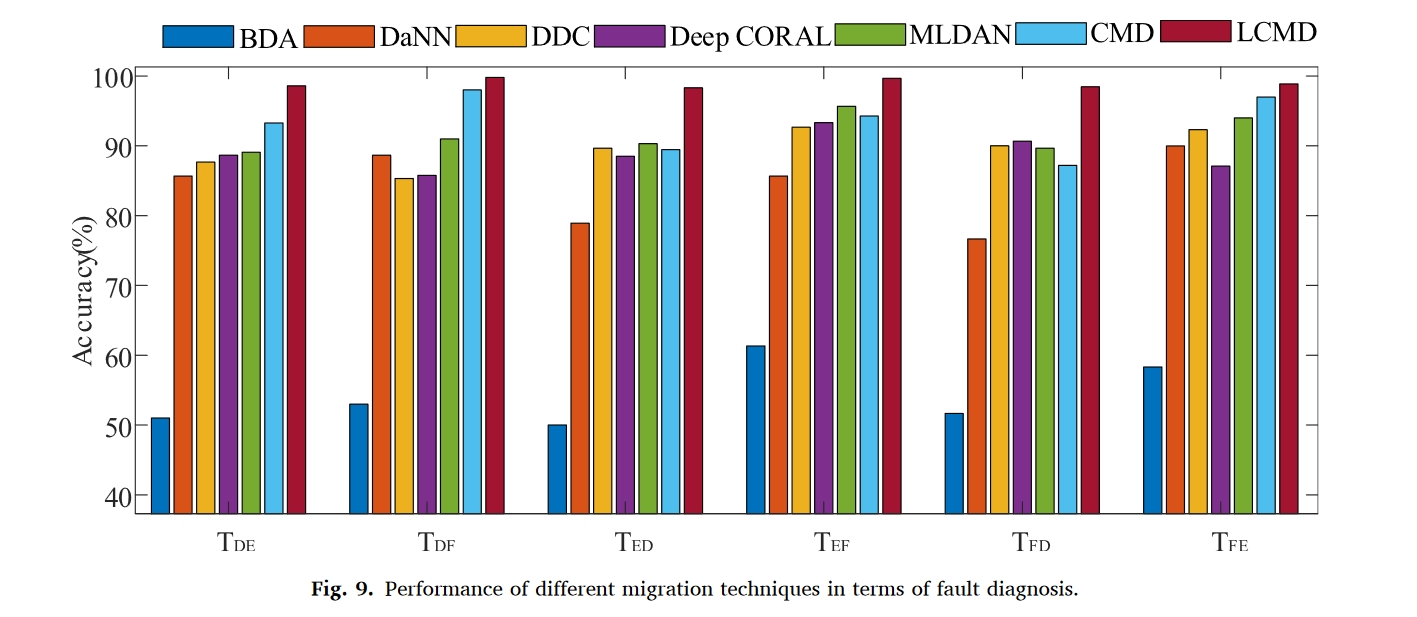
总结

本文提出了一种新的基于局部中心力矩偏差用于迁移学习的多尺度学习方法。

本文的两个点都是自己提出来的：

1. local central moment discrepancy（LCMD）
2. MS-CNN

LCMD相较于CMD，创新点主要是加了一个类别全重$w^c$，其表示批次中每个类别的百分比。

MS-CNN也是一种常规修改。