引言

1. 转动部件在各种工业环境中运用广泛，对其故障进行诊断非常重要。特别是，在数据驱动的框架下，基于深度学习的故障诊断可以大大减少对专家知识和工程经验的依赖，形成端到端的诊断系统

2. 现有的深度学习方法都基于训练数据集充分的前提，然后实际上有标签的真实数据非常有限。因此真实工业中的数据往往与训练数据集并不同分布。这会导致”分布外问题(OOD)”。那么该模型在真实诊断时就可能会”自信地”给出错误的预测结果并且没有任何预警。

3. 域迁移被提出来以解决训练数据集不足的问题，其主要包含参数迁移和域泛化两种方法。然而实际上它们实际上还是局限于具体的目标域，并没有完全解决分布外问题。

4. 为了形成可靠的故障诊断方法，智能模型不仅要关注诊断决策和准确性，还要评估其可信度，而这些在黑盒模型中被忽视了。应考虑一个额外的阶段，即可信分析，以检测先前未知数据的发生，从而对潜在的不可信诊断发出警告，并转向人类评估。OOD检测有可能实现可信分析，该分析旨在评估监测数据是来自与训练数据相同的分布，即ID数据是否来自不同的领域。

5. 最新的OOD模型主要包含:

   1. 基于softmax输出的方法(softmax output-based methods)
   2. 基于重建的方法(reconstruction-based methods)
   3. 基于不确定性的方法(uncertainty-based methods)

   本研究中提出的方法属于基于不确定性的方法。基于不确定性的OOD检测专注于开发高度准确的方法来量化OOD样本的预测不确定性现有的深度学习方法几乎没有进行这方面的研究，都是直接给出确定的答案。因此该文提出了一种基于集成深度学习网络的OOD研究方法。长期以来，人们一直认为，集成学习在诊断性能和泛化能力方面优于单一模型。

6. 在本研究中，提出了一种新的OOD检测辅助可信机械故障诊断方法，以标记和拒绝训练模型的OOD样本，从而避免不可信的诊断决策。主要贡献有两方面：

   1. 研究了一个潜在的重要新领域，即可靠的故障诊断。实现OOD检测是为了保证ID数据的可信诊断，并解决实际行业应用中看不见的故障诊断的挑战，这放宽了大多数智能故障诊断方法中的闭集假设。
   2. 描述了一种简单有效的DBL集合，它不仅能够准确诊断ID样本的健康状况，而且能够估计诊断过程中的预测不确定性。给出了一个合适的准则来自适应地确定不确定性阈值，从而可以自动识别出具有未知故障的OOD样本。

   方法

该文建立了一种深度集成网络。该网络由多个网络构成。而本文的基础假设就是不同的模型学习到的特征不一样，因此对于没有见过的信号，会产生不同的预测结果，而对于见过的信号，则会产生相同的正确的预测。因此本文的结构如下:

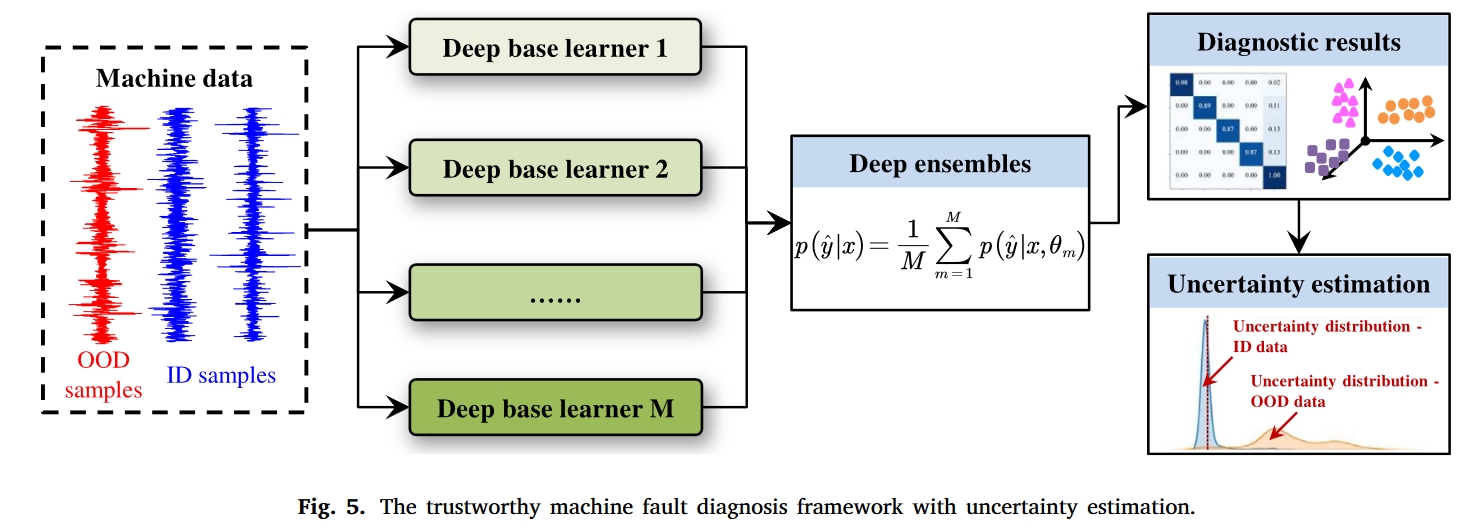
文中分别采用了下面5种网络来学习特征：

1. CNN3
2. CNN5
3. CNN7
4. ResNet
5. InceptionNet

不确定性的估计如下：

𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡, 𝜃1) = [1.0, 0.0]

𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡, 𝜃2) = [0.0, 1.0]

𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡, 𝜃3) = [1.0, 0.0]

𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡, 𝜃4) = [0.0, 1.0]

𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡, 𝜃5) = [1.0, 0.0]

则 -> 𝑝( ̂ 𝑦|𝑥𝑜𝑢𝑡) = [3∕5, 2∕5]

其中单个DBL的不确定性为零，而深系综的不确定性是一个大值，即”−3/5*log(3/5)−2/5*log(2/5)”。直观地，深度集成在不确定性估计方面的有效性得到了清楚的说明。

不确定度阈值的选择

不确定性可以告诉人类专家，诊断决定是可信还是不可信。前者通常会产生较低的不确定性，对决策具有较高的可信度，而后者则具有较高的不确定性，反映了模型在诊断过程中的未知性。为了自动判断诊断决策的可信度，需要确定一个适当的不确定性阈值来检测 OOD 样本。所需的不确定性阈值应大于大多数 ID 样本的不确定性阈值，但低于 OOD 样本的不确定性阈值。由于 OOD 样本在模型训练过程中是不可预见的，因此不确定性阈值只能在 ID 样本的验证集中确定。本研究采用四分位数区间（IQR）接近规则找出 ID 样本中不确定度值的上界，并将其设为阈值。不确定度阈值的计算公式如下:

𝐼𝑄𝑅 = 𝑄3 − 𝑄1

Upper bound = 𝑄3 + 1.5𝐼𝑄𝑅,

其中𝑄1和𝑄3分别是ID验证集中不确定度值的第一个四分位数和第三个四分位。

IQR近似规则有助于发现ID验证集中不确定性值的模式和异常值。该不确定性阈值可以确保大多数ID样本被认为是可信的，同时检测ID样本的异常值以及具有更高不确定性的OOD样本。

此处的不确定性阈值的作用在于当上面计算出的不确定大于这个阈值时，就视为该标签未见过。

实验

数据集

1. Wind turbine（自建）
2. Gearbox（自建）

结果

数据集1-Wind turbine

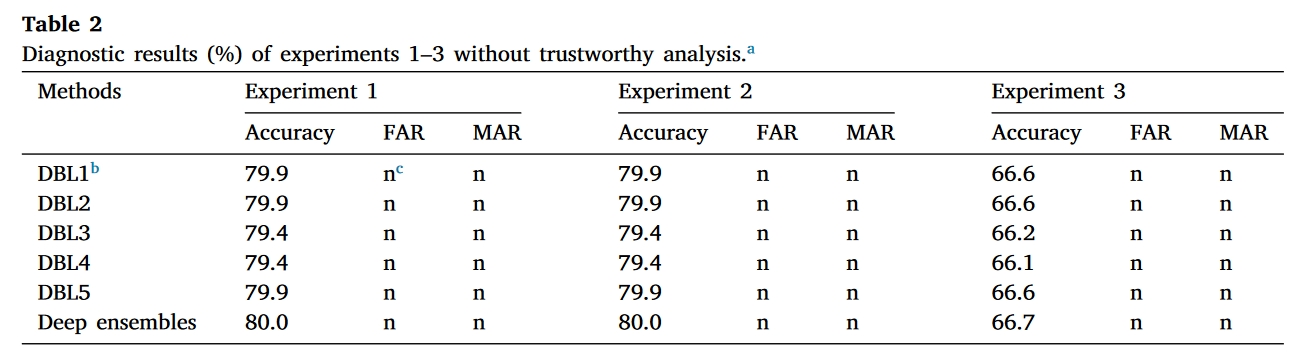
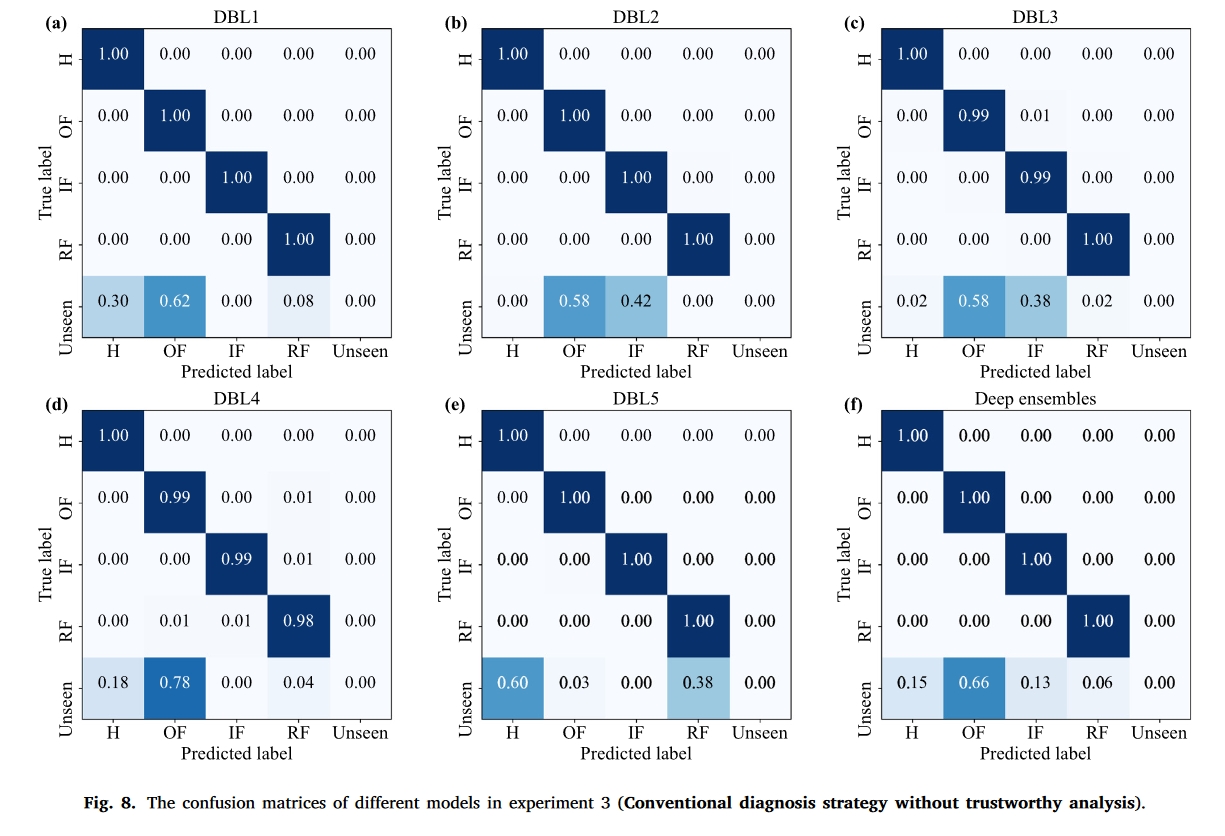
数据集2-Gearbox

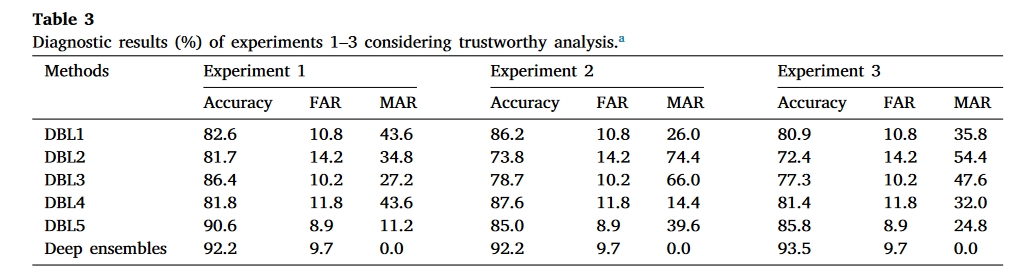
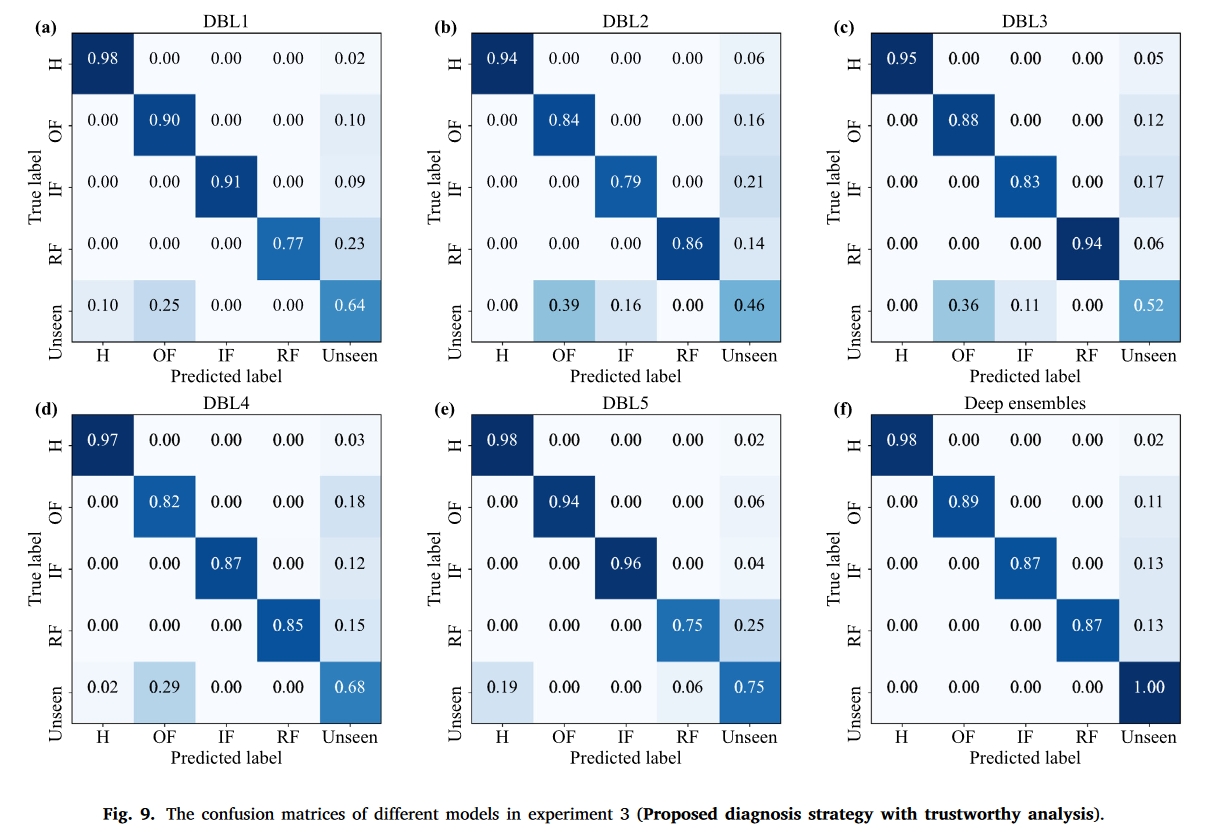
实验分析

可以看出，在第一个数据集中，准确率提升很小。并且从混淆矩阵中可以看出，分布外的样本并没有很好的被识别出来，这可以归结于下面结论中的问题。即多个网络可能学习到了同样的特征，因此集成过后效果并不佳，甚至大部分分布外元素都没有正确识别。

总结

该文的为了获取可信的故障诊断结果，建立了一个集成深度网络。主要原理是假设每个网络学习到的参数是不同的，因此不同的网络在面对见过的数据(即分布内数据)会获得相同的结果；然而在面对没见过的数据(即分布外数据)就会获得不同的结果。然后基于每一个模型的结果来获取可信值。

然而我认为本文还存在有些问题:

1. 本文的假设基础-不同的网络会从不同的角度学习特征，并不一定成立。文中给出的说明是使用使用不同的初始化和不同的网络结构以获得不同的特征学习角度。然而这个并不一定成立。不同网络从不同的角度学习特征实际上是一个经典的专家系统问题。后续可以从这个角度来改进该方法。