期刊: The International Journal of Advanced Manufacturing Technology (IF:3.4)
引言
- 旋转机械已朝着高速化、大型化、一体化的方向发展。轴承是旋转机械的重要部件。轴承的健康状况对机器的可靠性、稳定性和安全性有很大影响。
- 介绍了传统机器学习方法,并且其有以下两个缺点:
- 方法的上限性能基于手动选择的特征,这些特征依赖于大量的专业知识和广泛的数学知识。
- 高精度只能在特定条件下实现,因为模型是在特定特征类型下训练的。该模型在其他情况下可能表现不佳。
- 介绍了基于深度学习方法的故障诊断。
- 尽管如此,上述深度学习模型仍然存在两个缺点。
- 只有当训练集和测试集遵循相同的数据分布时,某些方法才能很好地执行。然而,由于操作条件的不同,训练集和测试集之间的分布可能会发生变化,这会导致方法的泛化能力下降。
- 在实际情况下,由于安全问题,故障数据极难获得,这使得标记的故障数据不足以用于测试集。
- 介绍基于域泛化的深度学习方法,同时指出现存方法的问题:
- 尽管许多领域自适应方法在故障诊断中取得了良好的效果,但很少有方法在不进行任何其他变换的情况下直接对原始时间信号进行自适应。
- 一些深度学习方法的结构复杂,导致计算效率低,耗时长。
- 根据相关实验,许多深度学习方法假设域偏移只影响深层的特征,但浅层的特征也会受到影响。仅在深层实现领域适应性是不够的。
- 针对上述问题,本文提出了一种新的多层自适应CNN(MACNN)方法。这项工作的主要贡献总结如下:
- 构造了一种新颖简单的深度学习算法,该算法通过使用多核MMD(MKMMD)和一种称为自适应批量归一化(AdaBN)的简单域自适应算法来实现域自适应。该方法防止了模型的浅层和深层中表示的域偏移。也不需要带标签的测试集。
- 构造了宽卷积核和具有残差结构的多尺度特征提取器,从多个尺度获得特征,以提高所提出方法的分类精度并加速收敛。
- 讨论了不同故障诊断任务中的最佳大量参数λ,以及样本量变化对该方法测试精度的影响。
相关研究
(Adaptive Batch Normalization) AdaBN
AdaBN是Batch Normalization(BN)的一个变种。
BN即对隐藏层的参数做批量归一化,而归一化就要用到训练集的数据分布信息,均值和方差。
但是传统的BN在训练和测试时使用的都是训练集的均值、方差等。对于传统深度学习,由于训练集和测试集来自同一数据集,都是同分布的,则没有问题。但是在迁移学习中,源域和目标域往往并不是同分布的,则期望使用测试集的均值、方差等来进行归一化。这就是AdaBN的原理。
AdaBN的主要步骤分为3步:
使用训练集进行model.fit。这一步和常规训练一样,但是绝对不能把测试集当验证集进行,这是常识性错误。
再次进行model.fit。这一步是最关键的,上一步我们相当于进行了正向传播和反向传播,并且保存了最佳模型的参数。这次fit中我们需要使用训练集(即目标域的测试集)进行正向传播,确保BN中的参数更新为测试集集相关的。这里如果使用pytorch的话据说非常简单,直接将BN层track_running_stats=True参数,把它改成False,这样在model.eval()时就是用目标域样本的均值和方差。
注意这一步仅仅更新BN层的参数,不能更新其他层的参数,因为这实际上是测试集。所以通常是要freeze其他层。
再使用测试集进行测试。
这样即为AdaBN,虽然BN层的方差和均值本来就是可得的,所以是没问题的。
MKMMD
MMD[21]是用于估计边际分布差异的非参数距离测度,如下所示:
$$\begin{aligned}
D_{H}^{2}(X^{s},X^{t})& =\left|\frac1{n_s}\sum_{i=1}^{n_s}\phi\left(X_i^s\right)-\frac1{n_t}\sum_{j=1}^{n_t}\phi\left(X_j^t\right)\right|H^2 \
&=\frac1{n_s^2}\sum{i=1}^{n_s}\sum_{j=1}^{n_s}k\left(X_i^s,X_j^s\right)+\frac1{n_t^2}\sum_{i=1}^{n_t}\sum_{j=1}^{n_t}k\left(X_i^t,X_j^t\right) \
&-\frac2{n_sn_t}\sum_{i=1}^{n_s}\sum_{j=1}^{n_t}k\Big(X_i^s,X_j^t\Big)
\end{aligned}$$
其中,$X_s$是源数据集,$X_t$是目标数据集,H是再现核希尔伯特空间(RKHS),$φ:X_s,X_t→ H$和$k(·,·)$是一个高斯核函数。
MKMMD[22]是MMD的扩展,它假设可以使用多个核的线性组合来获得最优核。高斯核的线性组合如下所示:
$$K|\triangleq\left{K=\sum\limits_{u=1}^m\beta_uk_u:\beta_u\ge0,\forall u\right}$$
其中$β_u$表示系数,$k_u$是核函数。
MACNN
实验流程:
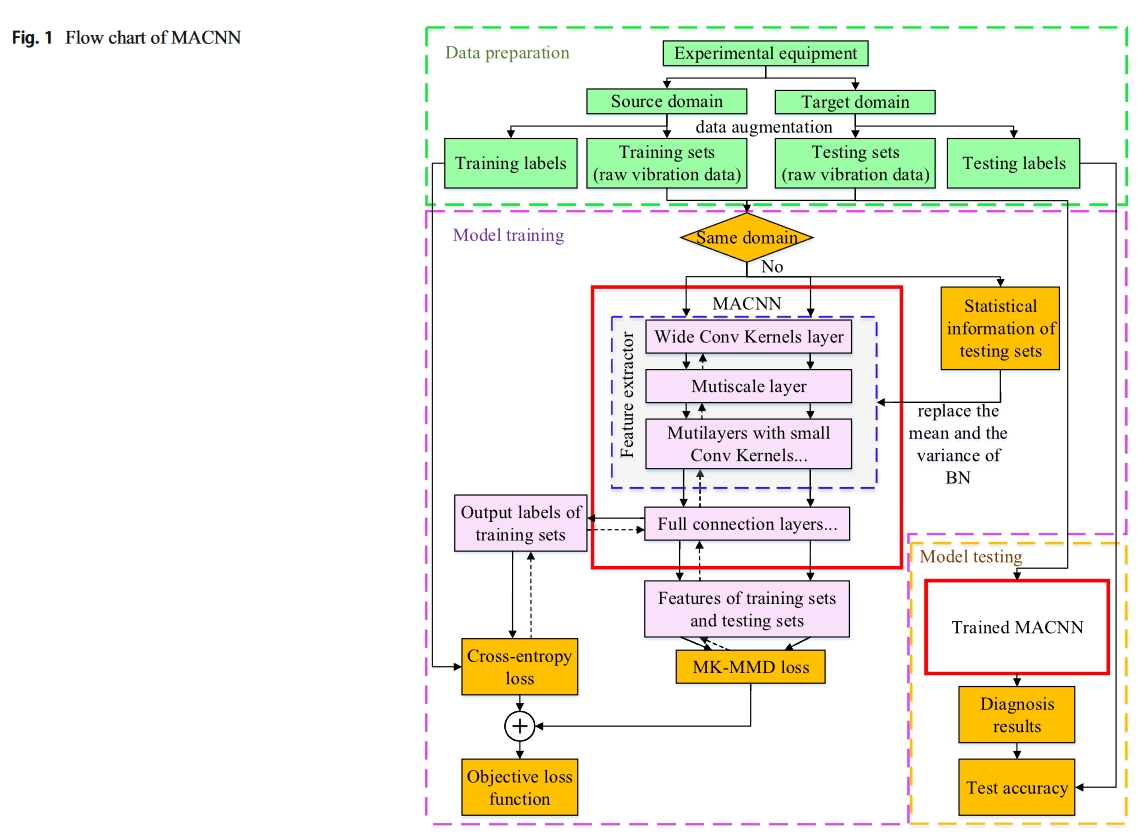
结构很简单,backbone采用MS-CNN,损失函数采用MKMMD和交叉熵。将BN替换成了AdaBN。
算法流程如下:
- 利用传感器采集不同条件下的振动信号,并使用数据增强技术对样本进行重叠切分,以增加样本数量
- 将带标签的源域样本和不带标签的目标域样本输入拟议方法进行模型训练
- 将带标签的目标域的样本输入训练好的模型,以获得预测标签,并将其与真实的标记标签进行比较,以进行验证。
网络结构:
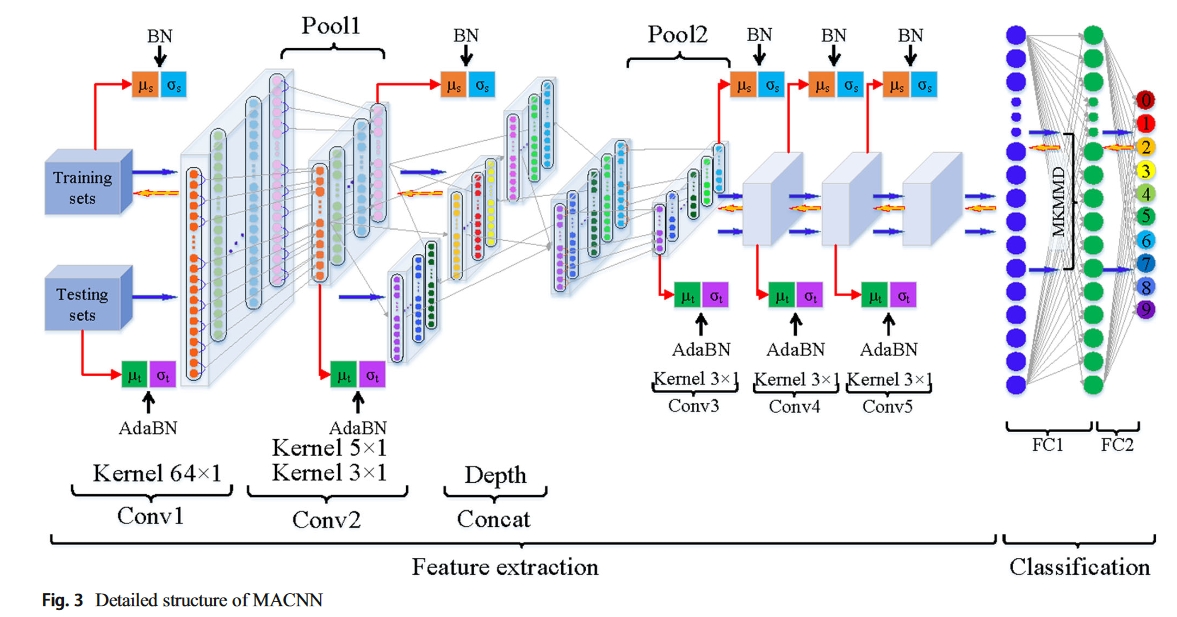
实验
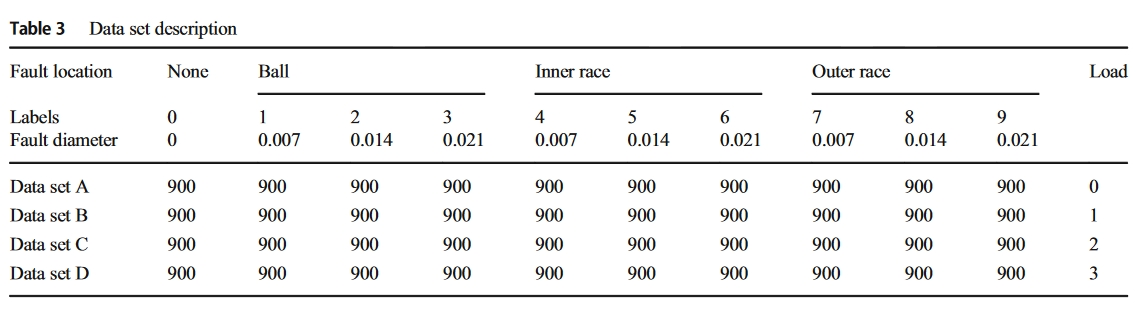
数据集
- CWRU
实验结果
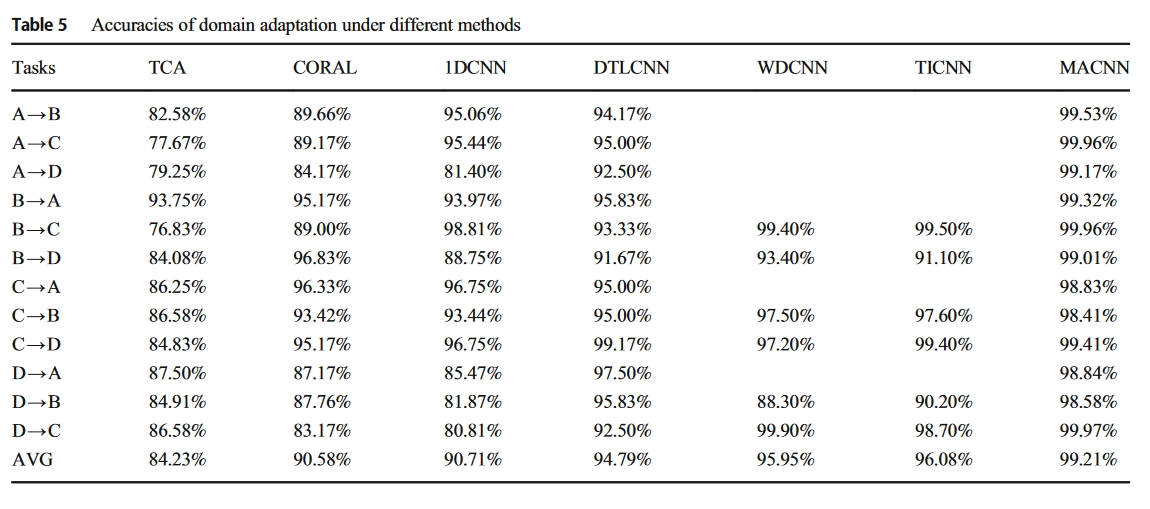
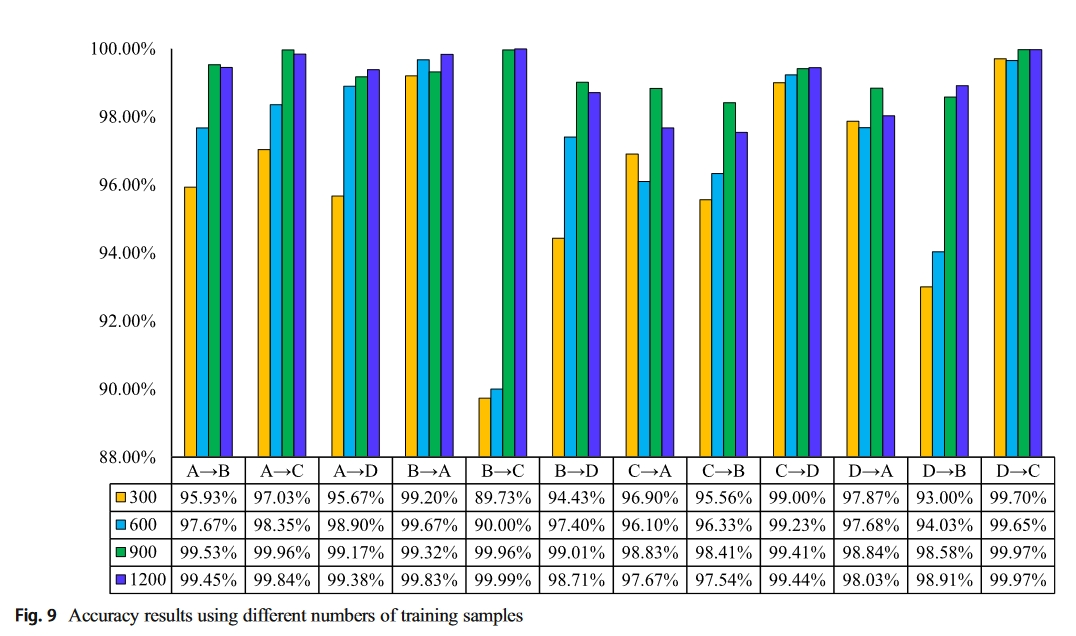
对比方法
- TCA:2011TNNLS
- CORAL:2016AAAI
- 2019:IEEE Sensor J
- 2018:Mech. Syst. Signal Process
总结
在多尺度的网络的基础上加了MKMMD和AdaBN。