引言

1. 轴承是列车运行系统中的关键部件，其状况对列车安全有着重要影响。对于实时故障检测和建立智能列车运行维护系统，研究轴承故障识别和提高识别效率至关重要。

2. 振动信号通常被用作列车轴承故障诊断的媒介。振动传感器采集的列车轴承振动信号往往是各种信号的调制和叠加，而现场采集的轴承信号大多是不平衡数据集，这给轴承故障特征提取和故障识别带来了很大困难。

3. 介绍了信号分析方法，比如EMD，EEMD和CEEMD。

4. 介绍了深度学习故障诊断方法。

5. 介绍了一维信号转换为二维图像的一些研究。

6. 由于从振动传感器获得的轴承振动信号经常与环境噪声、机械振动和异常振动信号相耦合，因此直接从原始信号中提取故障特征一方面增加了特征提取的难度，另一方面也增加了分类器的学习难度。

   1. 基于上述分析，利用CEEMD对轴承的振动信号进行分解，从中可以提取出包含异常信息的振动频带，并可以分离出包含故障信息的特征频带。

   2. 考虑到具有高相关性的IMF分量是多变量时间序列信号，基于多通道和MLP网络相结合的思想，提出了一种混合轴承故障识别方法。

算法

下图是本文提出算法的结构图：

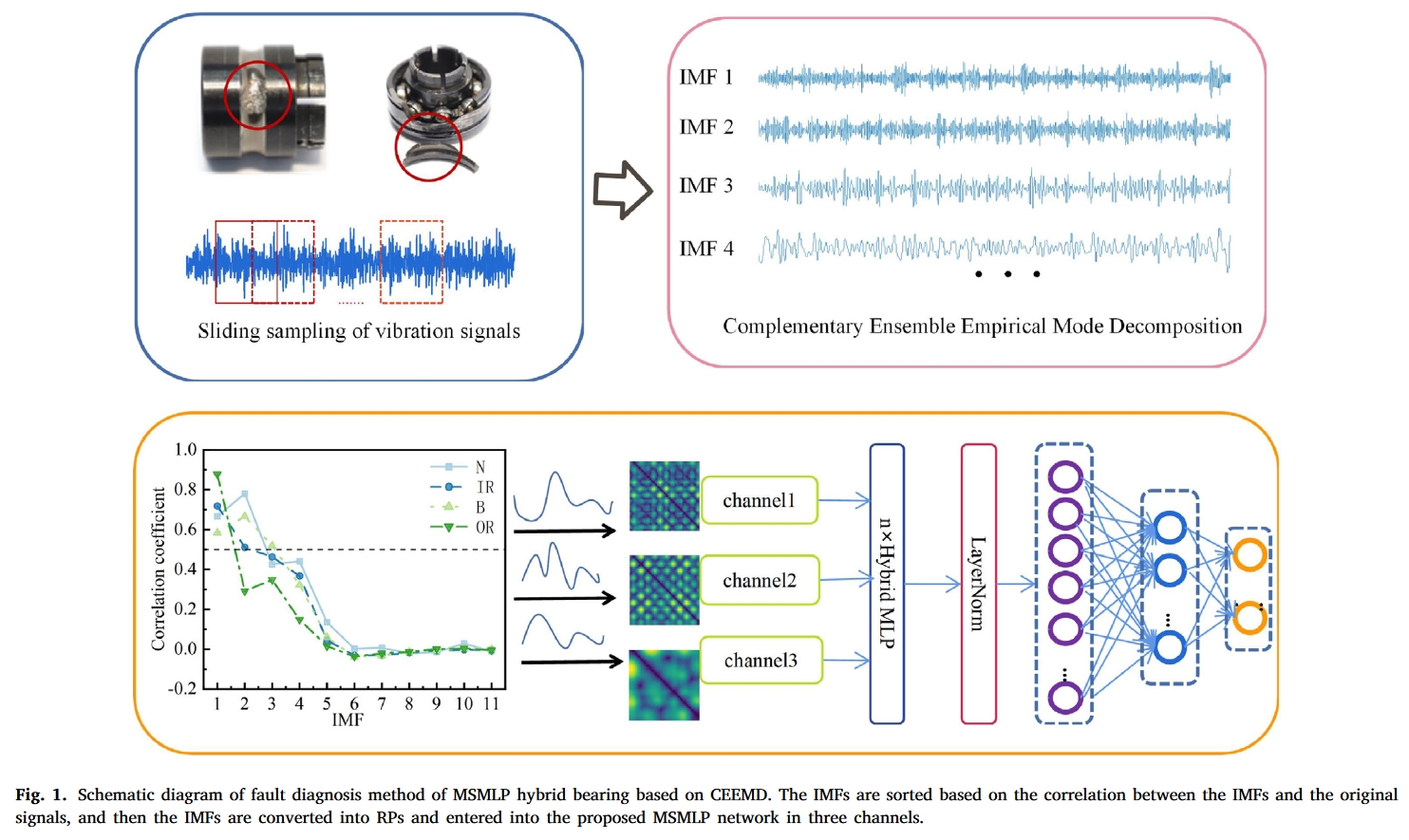
1. 首先，利用滑动窗口对轴承振动信号进行分割。然后，使用递归绘图方法将样本转换为二维数据。

2. 最后，处理后的样本被送往MSMLP进行测试和培训。下面将解释该方法的细节。

基于CEEMD的数据预处理

轴承振动信号主要包含结构噪声和环境噪声。为了减少噪声的影响，使用CEEMD对信号进行了预处理，本节将解释降噪预处理过程。

为了从轴承故障信号中提取出包含异常信息的振动频带，对原始信号进行预处理，筛选出包含故障信息的特征频带。已知样本的原始信号为$x(t)$，将互补高斯白噪声$n(t)$加到原始信号上，得到2n组新信号：

$x^+_i(t)=x(t)+n^+_i(t)$

$x^-_i(t)=x(t)+n^-_i(t)$

EMD用于分解并获得2n组IMF分量，这些分量被平均：

$imf_i=\frac{1}{2}(imf^+_i+imf^-_i)$

由此得到的$ imf_j $ 表示𝑥(𝑡) 被 CEEMD 分解后的各阶 IMF，其中 j 阶信号分解为特征模函数，j=1, 2, . , m.

从m阶IMF分量中提取高频分量和表示原始信号趋势的分量，即滤除轴承部件的固有振动和环境噪声信号等影响识别精度的分量。CEEMD对采集到的轴承振动信号进行预处理，将相关性较大的分量划分为多个通道进行输入网络。

递归图-一维转二维

递归图主要可以将非线性动力系统的行为可视化：它可以解释时间序列的内部结构：给出有关相似性、信息量和预测性的先验知识，是分析时间序列周期性、混沌性以及非平稳性的一种重要方法。

递归图是非平稳信号研究领域常用的处理与分析方法，其在机械探伤领域给予医学领域已有了成熟的应用。

构造递归图的关键是进行相空间重构。所谓相，是指某个系统在某一时刻的状态，系统所有可能出现的相组合统称为相空间。相空间重构则是通过应用相关方法和更改相关参数，对原相空间内的时域信息进行重新构造，通过一系列变换将信号提升至更高维度，使信号产生某种系统特性。

相空间重构需要选择合适的延迟系数τ、嵌入维度m和阈值ε。比较常用的嵌入维度选取方法有伪邻域法，延迟系数选取有平均互信息法，最佳递归阈值目前没有较好的方法，一般选择峰值的10%。

起算法步骤如下：


还有一些一维信号转二维图片：

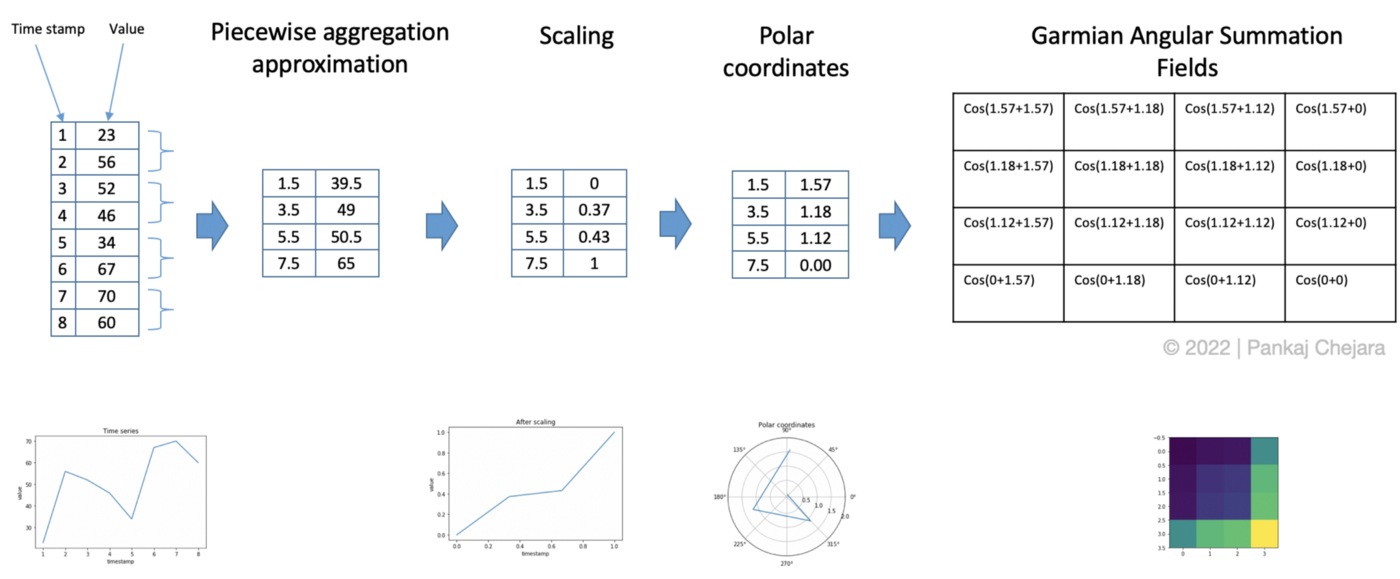
1. Gramian Angular Field, GAF（格拉姆角场）：利用极坐标和格拉斯坐标转变。

   1. 通过取每个 M 点的平均值来聚合时间序列以减小大小。 此步骤使用分段聚合近似 ( Piecewise Aggregation Approximation / PAA)。
   2. 区间[0,1]中的缩放值。
   3. 通过将时间戳作为半径和缩放值的反余弦（arccosine）来生成极坐标。 这杨可以提供角度的值。
   4. 生成GASF / GADF。 在这一步中，将每对值相加（相减），然后取余弦值后进行求和汇总。

   

2. Markov Transition Field （马尔可夫变迁场）：马尔可夫转变场是从时间序列获得的图像，表示离散时间序列的转变概率场。可以使用不同的策略对时间序列进行分类。

Architecture of MSMLP

NeurIPS2021年上的文章《MLP-Mixer: An all-MLP Architecture for Vision》提出了一个通过简单的mlp层堆叠而成的模型：MLP-Mixer。该模型在精度与卷积神经网络、视觉Transformer相似的情况下更高效。本文也算是follow这个工作，所以仅仅用了多层MLP。

MLP-Mixer中的网络如下：

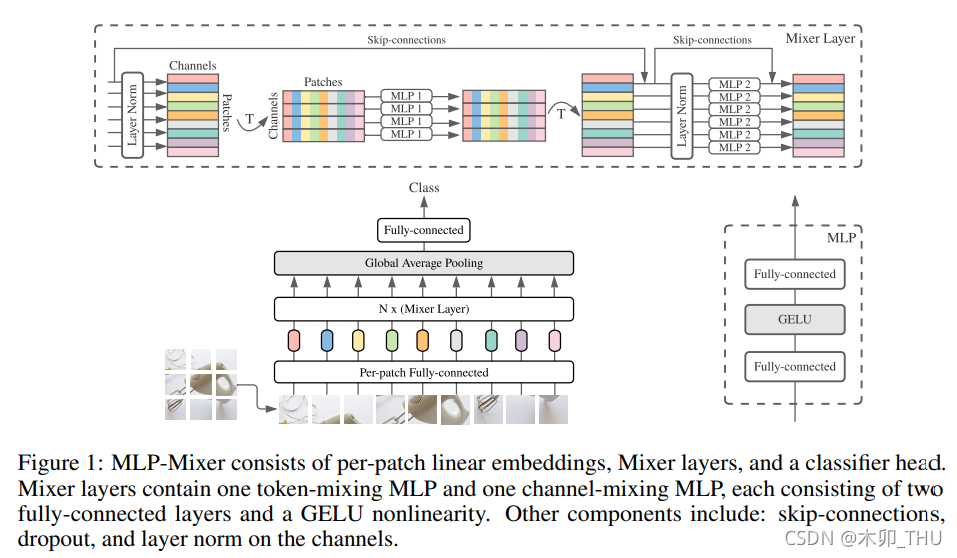
该文中不是简单的使用MLP，而是设计了一种新的操作，成为Mixer Layer，

具体操作为：

1. 假设我们有输入图像 224 × 224 × 3 ，首先我们切 patch，例如长宽都取 32，则我们可以切成 7 × 7 = 49个 patch，每个 patch 是 32 × 32 × 3。我们将每个 patch 展平就能成为 49 个 3072 维的向量。通过一个全连接层（Per-patch Fully-connected）进行降维，例如 512 维，就得到了 49 个 token，每个 token 的维度为 512。然后将他们馈入 Mixer Layer。
2. 细看 Mixer Layer，Mixer 架构采用两种不同类型的 MLP 层：token-mixing MLP 和 channel-mixing MLP。
   1. token-mixing MLP 指的是 cross-location operation，即对于 49 个 512维的 token，将每一个 token 内部进行自融合，将 49 维映射到 49 维，即“混合”空间信息；
   2. channel-mixing MLP 指的是 pre-location operation，即对于 49 个 512 512512 维的 token，将每一维进行融合，将 512 维映射到 512 维，即“混合”每个位置特征。为了简单实现，其实将矩阵转置一下就可以了。这两种类型的层交替执行以促进两个维度间的信息交互。单个 MLP 是由两个全连接层和一个 GELU 激活函数组成的。
3. 此外，Mixer 还是用了跳跃连接（Skip-connection）和层归一化（Layer Norm），这里的跳跃连接其实不是 UNet 中的通道拼接，而是 ResNet 中的残差结构，将输入输出相加；而这里的层归一化与 DenseNet 等网络一致，作用于全连接层前面，进行前归一化（DenseNet 的 BN 层在卷积层前面，也有工作证明 LN 在 Multi-head Self-Attention 前会更好）。

具体见这里，感觉可以follow。

输入部分，每个信号片段经过CEEMD分解后有n个IMF，这些IMF经过PR预处理后得到n张图片，则将这些图片作为该信号片段的多个通道输入神经网络。

网络结构如下：

1. n个混合MLP：即上面的Mix Layer
2. 一个LayerNorm层
3. 一个LeakyRelu层
4. 和一个Droupout层

结构图（其实就是Mix MLP的结构）：

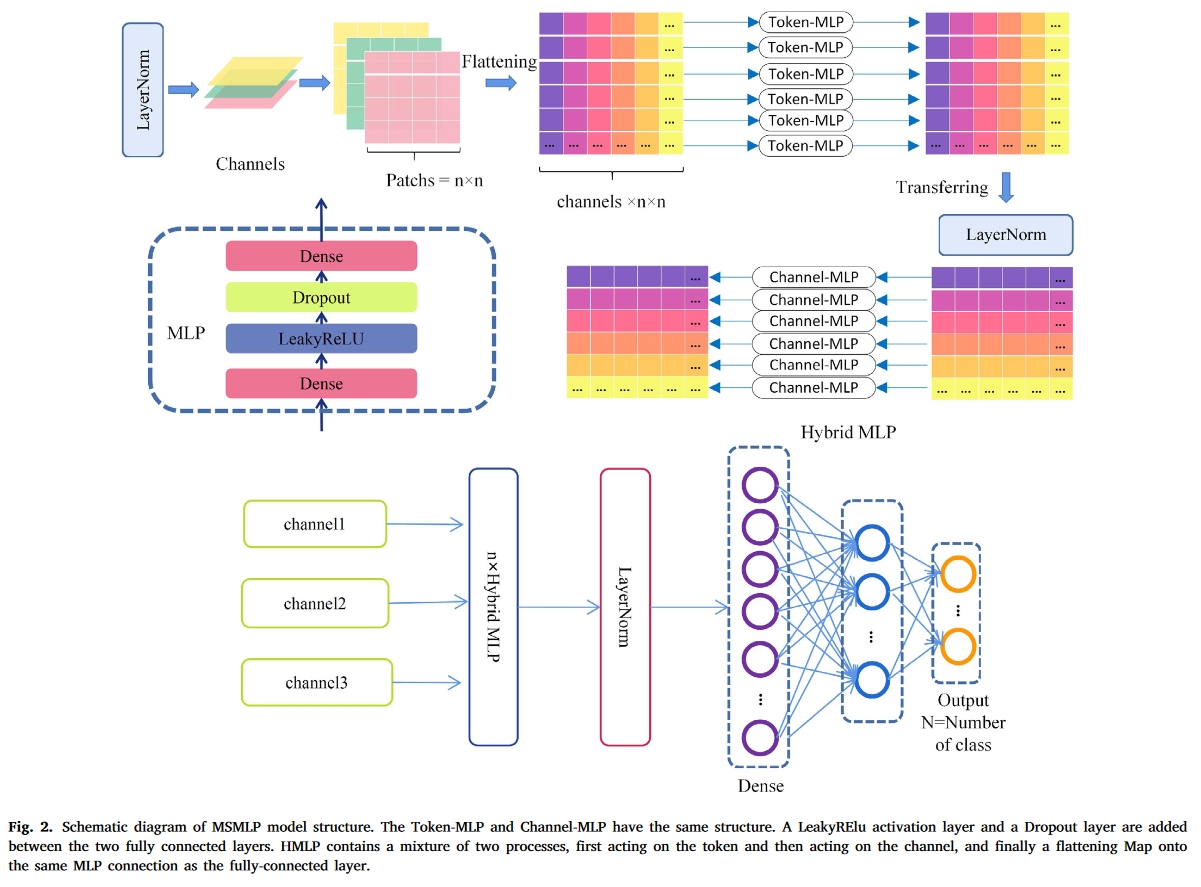
实验

数据集

1. CWRU
2. XJTU
3. CSU

实验结果



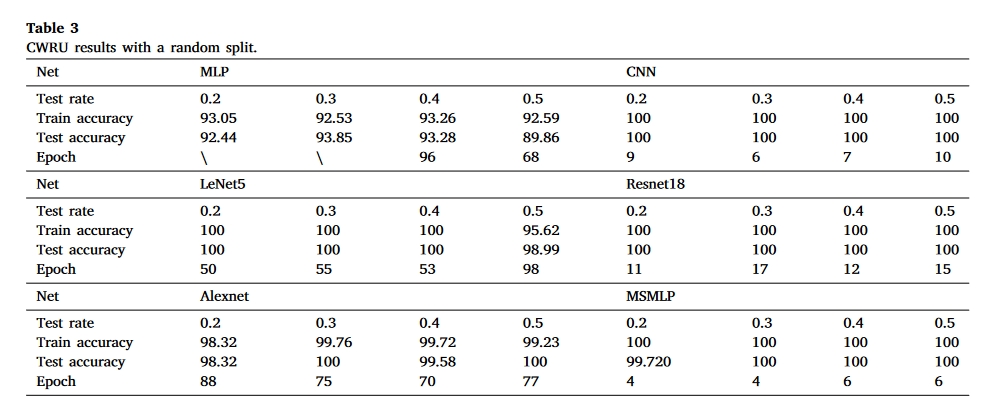
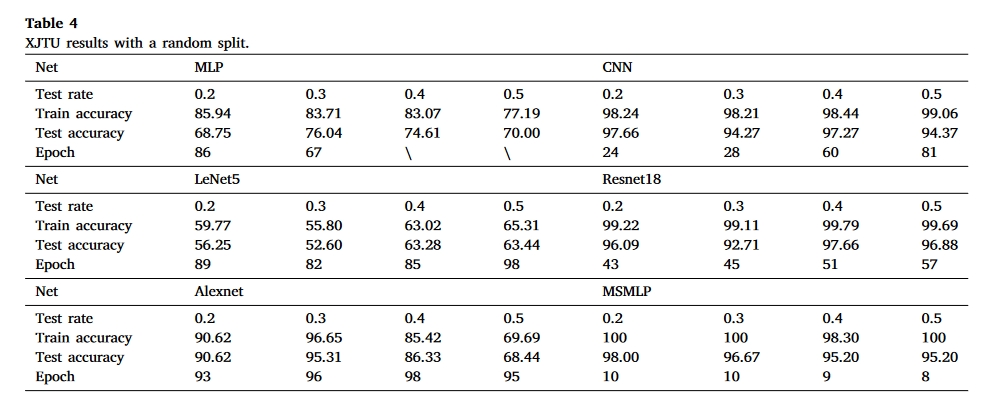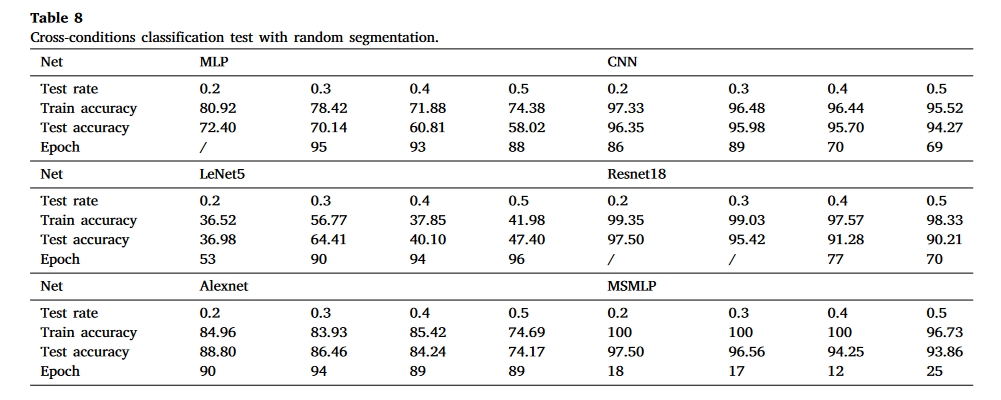
总结

本文也算是追热点的一篇文章，Transformer团队在NeurIPS2021上提出了Mix-MLP。而本文所谓的multi-scale，也只是用了CEEMD（CEEMD）使用了多尺度交叉熵。本质上提出了一个pre-processing+feature extractor的framework，没有对网络本身提出改进。