期刊: Neurocomputing (IF:6)
引言
- 介绍了转子部件的重要性,容易损坏。然后介绍机器学习算法在故障诊断中的应用。提出问题:这些方法都是利用各种信号处理算法人为地从原始振动信号中提取出来的,并没有充分利用 ML 中的智能算法。
- 介绍了深度学习算法在故障诊断领域的应用,比如SAE,CNN,DBM和HDN等。
- 介绍了CNN在故障诊断领域取得了很大的成就。
- 着重介绍了一般的故障诊断的CNN都是将一维信号转变为二维信号。但是也有1D CNN,然后提出了Deep Convolutional Neural Networks with Wide First-layer Kernels (WDCNN) model。这个模型在第一层使用了一个256的大卷积核用于抑制背景噪声的影响;然后采用几个小的卷积核进行特征提取和表达。实验结果表明,WDCNN模型在噪声环境中具有较强的鲁棒性。
- 介绍了CNN,GRU等,但是也提出了他们的问题:
- CNN中的Pooling层会导致平移不变性(非等价性)和信息丢失的缺陷。此外,池化操作可能会导致模型忽略整体和部分之间的关联。然而,去除池化层会带来一个新问题:感受野太小。
- 关于RNN,无论是普通RNN-LSTM还是GRU都没有完全解决长期依赖性问题,这表明RNN在长序列建模方面仍然存在不足。然后,RNN由于其计算状态的固有特性,也很难并行化,因此很难扩展。
- 介绍了注意力机制和Transformer的历史。然而,尽管变压器在CV和NLP方面取得了很大进展,但在故障诊断领域尚未得到广泛应用。
- 本文的目的是开发一种新的旋转机械故障诊断方法。将原始振动信号用于旋转机械故障诊断,提出了Time Series Transformer(TST)模型,该模型以注意力机制为核心,克服了传统CNN和RNN模型的平移不变性和长期依赖性问题。此外,设计了一种新一代的令牌序列模型,称为时间序列令牌化器,在此基础上,TST可以直接将1D格式的时域振动数据作为输入,而无需预处理。通过设置适当的训练过程,建立了一种无预处理的故障诊断方法。如后所述,使用这种新方法,可以直接使用原始振动信号在给定数据集上实现高精度的旋转机械故障诊断,而不需要任何预处理技术。
Time Series Transformer
然而,NLP中使用的香草变换器模型的输入是分词后的文本序列,并且CV中采用的视觉变换器(ViT)的处理对象通常是3通道RGB图像,因此不能直接处理振动信号。
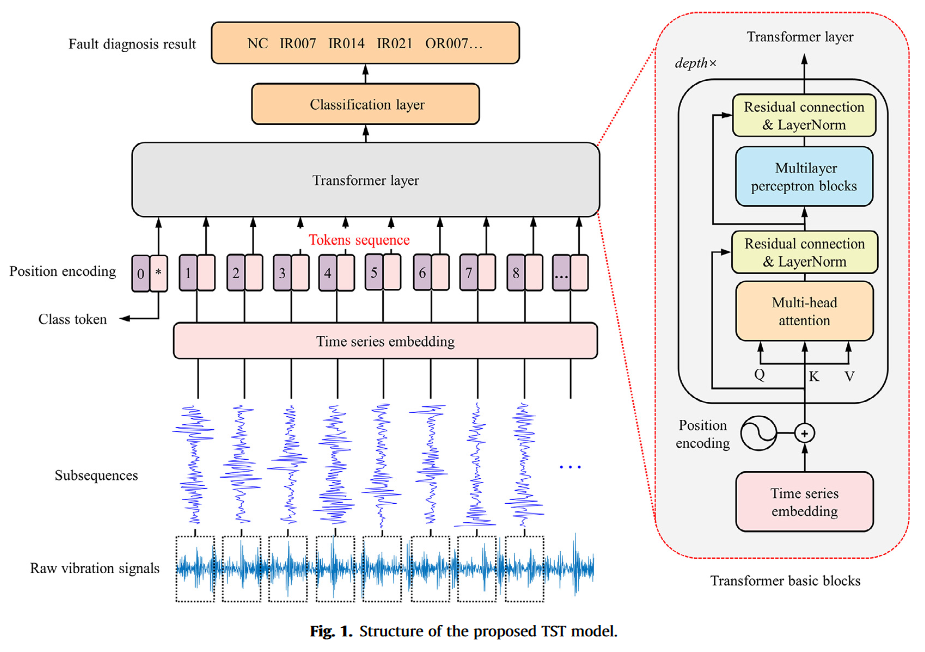
Time series tokenizer
本文将Transformer层的输入定义为令牌序列。所提出的TST利用时间序列标记器从原始振动信号中获得标记序列。
Time series embedding
具有批次的时间序列数据原则上可以表示为$t \in R^{B\times L}$,其中B是批量大小,L是给定振动信号时间序列的长度。输入时间序列被修剪成具有给定长度的几个子序列,并被拼接成表示为$[t^1_s, t^2_s, t^3_s,…,t^N_s,]$,其中$N_s$是划分的子序列的数量。然后,像单词嵌入一样,通过简单的线性变换将子序列映射到高维嵌入空间,可以给出为等式1:
$TokensSeq=[t^1_s, t^2_s, t^3_s,…,t^N_s,] \cdot W_{embedding} \in R^{B \times N_s \times dim}$
其中 $W_embedding \in R^{B \times B \times N_s \times dim}$ 是可学习矩阵,dim是时间序列嵌入的维数。需要指出的是,所有子序列共享相同的线性映射矩阵,以便TST学习更通用的映射。此外,时间序列嵌入的整个过程相当于对输入时间序列进行多通道1D卷积运算。然而,这并不意味着所提出的TST包含卷积层。
时间序列嵌入也可以看作是从输入振动信号中提取特征的过程。与CrossViT中嵌入具有不同补丁大小的输入图像的方法类似,当子序列的长度较小时,时间序列嵌入可以更好地提取时间序列的局部特征;相反,时间序列嵌入可能集中在全局特征上。
class token
所提出的TST需要在从令牌序列中提取特征之后表示特征。主要有两种方法:一种是对最后一个Transformer层进行全局池化;另一种是通过参考BERT在令牌序列中添加类令牌来获得特征图。类令牌是一个随机初始化的可学习序列,表示为$x_0 \in R^1\times dim$,并且具有类令牌的令牌序列定义为:
$TokensSeq=[x_0; [t^1_s, t^2_s, t^3_s,…,t^N_s,] \cdot W_{embedding}] \in R^{ B \times (N_s+1) \times dim}$
上式表明,经过多头注意力机制的计算,$x_0$与所有子序列相关,这意味着$x_0$融合了所有子序列的特征,因此可以采用$x_0$作为特征图。
Position encoding
由于所提出的TST中没有卷积运算,并且多头自注意机制在计算过程中不包含令牌序列中的位置信息,因此添加了位置编码以保留令牌子序列中的绝对和相对位置信息,这可以通过下式获得。
$TokensSeq=[x_0; [t^1_s, t^2_s, t^3_s,…,t^N_s,] \cdot W_{embedding}] + E_{pos} \in R^{ B \times (N_s+1) \times dim}$
其中$E_{pos}\in R^{ B \times (N_s+1) \times dim}$。这里用的是1D位置编码,更适合序列信息。
实验
数据集
- CWRU dataset
- XJTU dataset
- UCOON dataset
| dataset | train | test |
|---|---|---|
| CWRU | 7000 | 2000 |
| XJTU | 2800 | 1200 |
| UCOON | 655 | 281 |
CWRU dataset
| Methodology | Signal processing | Accuracy |
|---|---|---|
| LS-SVM [40] | EMD (Empirical Mode Decomposition) and PSO | 89.50% (4 categories) |
| ICDSVM [41] | EEMD (Ensemble Empirical Mode Decomposition) | 97.75% (4 categories) |
| BPNN [42] | Frequency spectra | 81.35%(10 categories) |
| DBN [43] | Time- domain features and PSO | 88.20% (10 categories) |
| CNN (1D format) [44] | Raw vibration signals | 93.30% (4 categories) |
| WT-CNN (2D format) [45] | Times-frequency domain images by WT (Wavelet Transform) | 95.09% (4 categories) |
| MC-CNN (1D format) [46] | Raw vibration signals | 98.46% (4 categories) |
| RNN [47] | Local features of the time-domain signals | 95.60% (4 categories) |
| LFGRU [47] | Local features of the time domain signals | 99.60% (4 categories) |
| CNN1D | Raw vibration signals | 97.32%(10 categories) |
| RNNLSTM | Raw vibration signals | 92.07% (10 categories) |
| ConvRNN | Raw vibration signals | 94.74% (10 categories) |
| TST (Proposed) | Raw vibration signals | 98.63% (10 categories) |
| 99.72% (4 categories) |
XJTU
| Methodology | Signal processing methods | Accuracy |
|---|---|---|
| NKH-KELM [48] | Multiscale Dispersion Entropy (MDE) | 95,.56% |
| CWT-CNN (2D format) [49] | Times frequency domain images by wT | 99.40% |
| DCN [50] | Raw vibration signals | 99.31% |
| VMD-CNN [51] | Variational Mode Decomposition (VMD) | 97.00% |
| AlexNet [52] | The short -time Fourier transform (STFT) | 99.58% |
| LSTM [52] | The short-time Fourier transform (STFT) | 98.65% |
| 1DCNN-LSTM [53] | Raw vibration signals | 98.32% |
| CNN1D | Raw vibration signals | 98.00% |
| RNNLSTM | Raw vibration signals | 94.08% |
| ConvRNN | Raw vibration signals | 95.33% |
| TST (Proposed) | Raw vibration signals | 99.78% |
UCOON dataset
| Methodology | Signal processing methods | Accuracy |
|---|---|---|
| AE | Frequency domain signals obtained by FFT | 95.13% |
| DAE | Frequency domain signals obtained by FFT | 93.76% |
| BPNN | Frequency domain signals obtained by FFT | 95.13% |
| Local CNN (2D format) | Images of the raw vibration signals | 97.57% |
| ResNet18 | Time domain sample reshape to a 2D matrix | 85.84% |
| LSTM | Frequency domain signals obtained by FFT | 88.74% |
| CNN1D | Raw vibration signals | 97.50% |
| RNNLSTM | Raw vibration signals | 93.59% |
| ConvRNN | Raw vibration signals | 96.44% |
| TST (Proposed) | Raw vibration signals | 99.51% |
启示
- 了解了Transformer在故障诊断领域的基本运用方法
- 本文的写作结构可以借鉴,方法论直接作为第二章,并没有按第二章related works,第三章提出的方法这种结构来写。可能也因为本文的创新很小,单独写一章可能不够。
- 本文与其他方法对比的时候,仅仅对比了引用的结果,其实训练集,测试集等可能都不一样,这也是一种避免复现别人论文的方法。