A-multi-layer-spiking-neural-network-based-approach-to-bearing-fault-diagnosis
日期: September 6th 2024, 5:24:25 am
期刊: Reliability Engineering & System Safety (IF:8.1)

引言

  1. 转子容易损坏，因此对其进行诊断很有必要。
  2. 故障诊断方法：
    1. 模型驱动方法
    2. 数据驱动方法
      1. 机器学习方法
      2. 深度学习方法
        1. 1DCNN
        2. 2DCNN
  3. 介绍脉冲神经网络：脉冲神经网络 (Spiking Neural Network，SNN) ，旨在弥合神经科学和机器学习之间的差距，使用最拟合生物神经元机制的模型来进行计算，更接近生物神经元机制。SNN 使用脉冲——这是一种发生在时间点上的离散事件——而非常见的连续值。每个峰值由代表生物过程的微分方程表示出来，其中最重要的是神经元的膜电位。本质上，一旦神经元达到了某一电位，脉冲就会出现，随后达到电位的神经元会被重置。
  4. SNN有有监督和无监督两种训练方法。第一次将脉冲神经网络引入到故障诊断领域。
  5. 提出传统神经网络需要大量的训练数据和训练时间，而相反，由于SNN中脉冲序列的节奏稀疏性，每个脉冲都包含高信息含量，使SNN能够显著减少用于训练的数据量，并使SNN更适合嵌入工业场景中的便携式硬件设备。
    1. 由于BP算法不能直接运用到SNN中。概率脉冲神经元模型（pSNM）以概率的形式表示神经元的信息传输过程，是解决SNN模型中脉冲序列不连续问题的替代方案。
    2. 然而，面对复杂的工作条件，由于多层学习算法尚未在pSNM中定义，因此仍然很难将pSNM扩展到更深层次。因此，本文提出了一种改进的学习算法和基于概率脉冲响应模型的多层SNN，以便于轴承故障诊断。

创新点

  1. 在这项工作中，所提出的多层SNN模型可以被视为第三代深度神经网络，因为它使用PSRM扩展了单层SNN模型。在所使用的数据集上实现了轴承故障诊断的最优性能。
  2. 通过将0–1脉冲序列转换为脉冲概率序列，提出了一种新的脉冲编码方式，以消除多层SNN在反向传播过程中的不可微问题。此外，通过输出尖峰神经元的膜电压，所开发的多层SNN还为轴承故障诊断中的不同故障模式提供了透明度。
  3. 基于PSRM，提出了一种多层SNN学习算法来简化多层SNN训练。

方法

fig.1

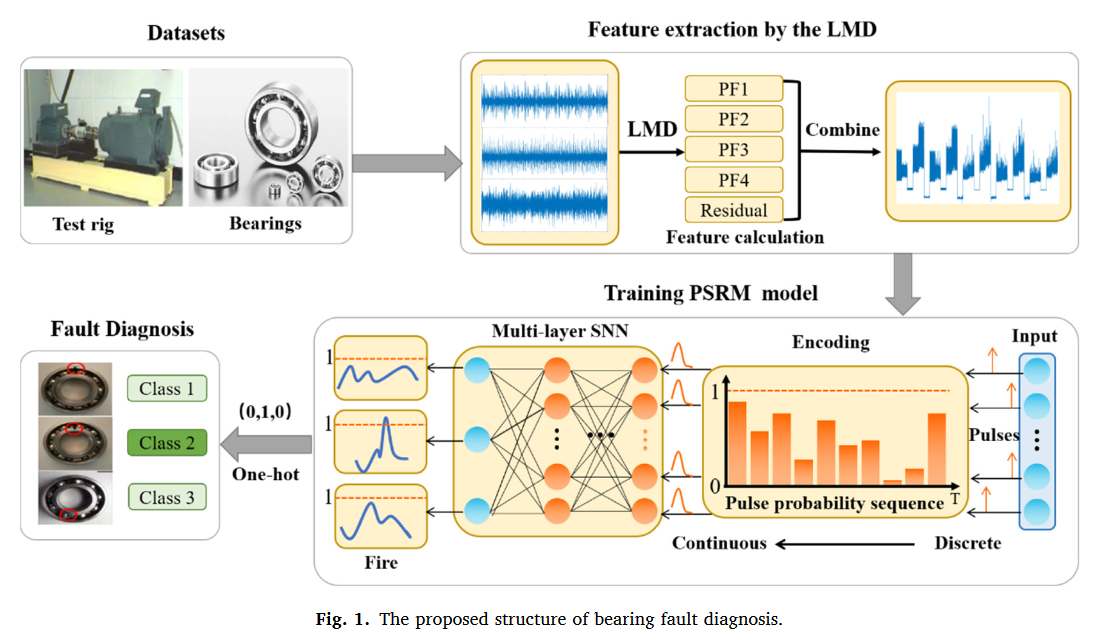
1. 使用LMD进行特征提取

由于原始振动信号中不可避免地会受到间隙、载荷和摩擦等非线性因素的影响，大多数振动信号不能满足稳定性和线性度的要求。此外，多层SNN只接受脉冲序列输入，这很难从原始信号中提取。

  1. FT不足以处理非平稳信号。此外，FT只能确定信号段中包含的频率分量，但故障特征通常隐藏在信号的局部范围内。
  2. WT具有尺度收缩的特性，可以捕捉信号的局部相似性。然而，它会导致频率基准不一致，导致物理解释不佳。
  3. 对于EMD，当信号中存在脉冲干扰和噪声时，分解信号将表现出模式混合。
  4. 利用LMD，可以将复杂的非平稳非线性信号分离为具有瞬时频率物理意义的PFs集合。

关于LMD算法：见这里。

多层SNN

SNN来源于生物神经元的结构，它们通过突触连接和传递信息。突触前神经元用于发送信息，突触后神经元用于从突触接收信息。该信息以动作电位或脉冲的形式表示。

编码

通常，传统的神经网络神经元通过特定的实数值传递信息，而生物神经元通过0-1个激发脉冲序列传递信息。在SNN中，发送脉冲时神经元的动作电位为1，否则不发送脉冲。

  • 这使得 SNN 只需通过 0 或 1 传输信息，从而大大降低了存储成本。
  • 因此，要通过多层 SNN 实现轴承故障分类，需要采用适当的脉冲编码方法将每个样本转换成一系列脉冲。
  • 然而，由于脉冲序列的不连续性，传统的 BP 算法无法直接用于多层 SNN 的训练。
  • 一种新的脉冲概率序列表示方法来消除这种不连续性。

fig.4

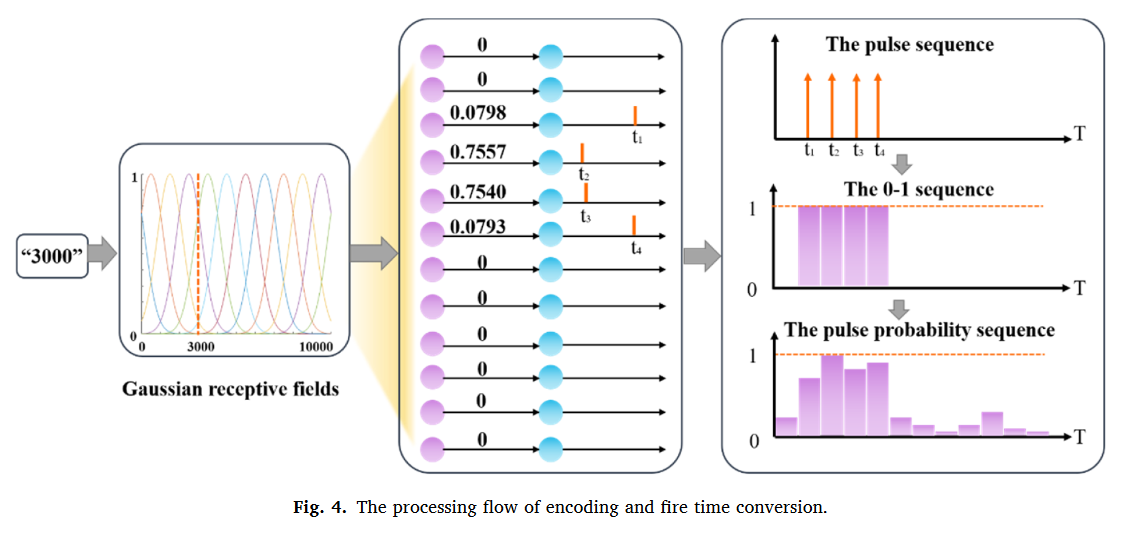
PSRM神经元模型

PSRM的膜电压定义为：

eq.16

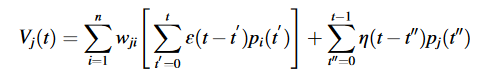
pi(t′)和pj(t′′)分别表示突触前神经元向t′发射的概率和突触后神经元向t’发射的概率；

ε（.）和η（.）可以分别定义如下：

eq.17

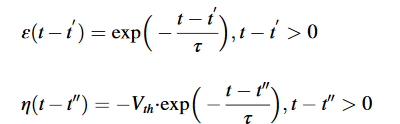
多层SNN学习算法

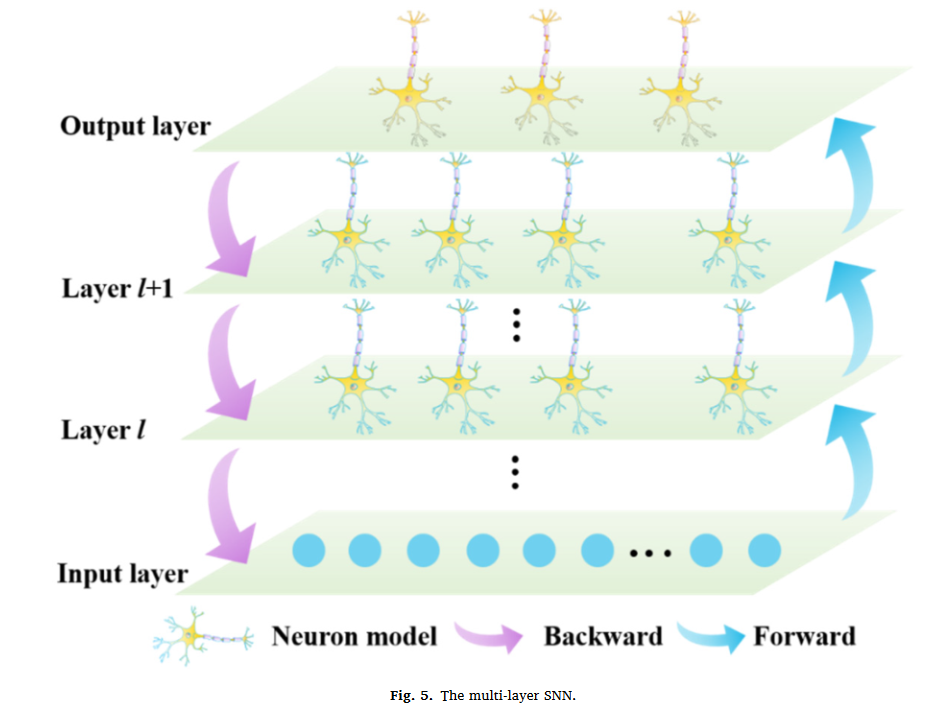
本文开发了多层学习算法，将BP算法应用于多层SNN，以实现更复杂、更实用的学习任务。具体而言，如图所示，多层SNN由一个输入层和一个具有多个隐藏层的输出层组成。每个隐藏层中的神经元数量是相同的，而相邻的两层是完全连接的。在分类问题中，网络的第一层表示初始特征向量，其中每个神经元表示一个特征。输出层给出了网络的预测结果。此外，突触神经元只有在接收到脉冲时才被计算，也就是说，下一层的神经元不需要计算与不发射脉冲的前一层神经元的连接权重。

fig.5

假设PL和Pd分别是样本的预测概率脉冲序列和参考脉冲概率序列。多层SNN的损耗函数可以定义如下：

eq.21

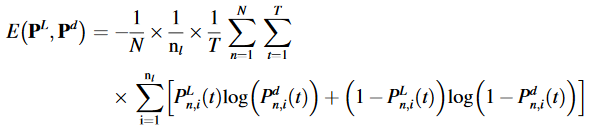
则灵敏度δli（t）和权重突触Δwji的调整可以分别定义如下：

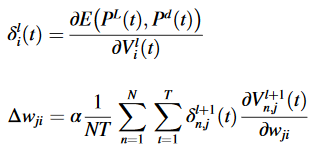
fig.22

则参数更新可以表示为：

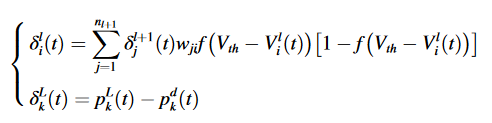
fig.24

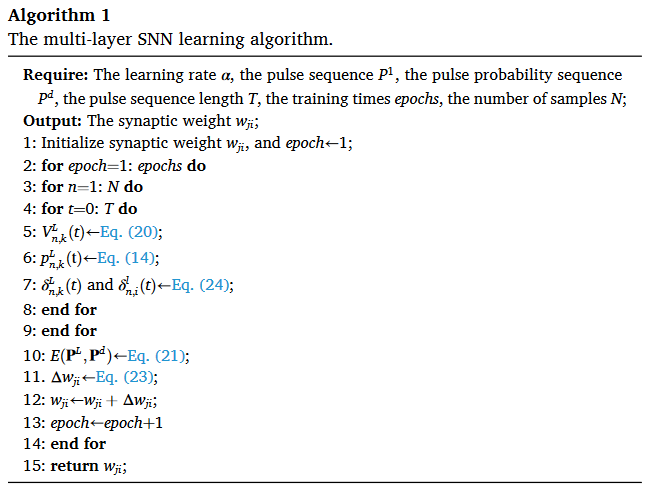
所以多层SNN学习算法的伪代码如下：

alg.1

实验

数据集

  • Case Western Reserve University
  • MFPT dataset
  • Paderborn University dataset

实验结果

CWRU数据集的结果

Trial index 1 2 3 4 5
Training 100.00 100.00 100.00 99.48 99.74
Testing 97.92 98.96 100.00 100.00 100.00

MFPT数据集的结果

Trial index 1 2 3 4 5
Training 99.65 99.13 99.31 99.48 99.83
Testing 99.31 100.00 99.31 100.00 100.00

帕德博恩大学数据集结果

Trial index 1 2 3 4 5
Testing 43.75 87.50 83.33 84.03 81.25

对比最新方法-MFPT

Methods Feature extraction methods Training sets Testing sets Accuracy (%)
CNN - - - 98.00~99.00
DCNN WT 7566 3242 91.30
STFT 99.90
HHT 92.90
Multi-layer ANN LMD 1176 144 99.31
SNN LMD 576 144 99.31
Proposed method LMD 576 144 99.72

对比最新方法-CWRU

Methods Feature extraction methods Training sets Testing sets Accuracy (%)
MPA-SVM GCMWPE 80 240 97.92
ANN Singular spectrum analysis 336 144 96.53-100.00
ANN Zero-crossing - 91.50-97.10
LiftingNet Layer-wise feature 800 800 99.63
CNN based Markov model CNN + HMM 9600 4800 98.13
Ensemble CNN and DNN CNNEPDNN 2000 370 97.35
SNN LMD 384 96 98.95
Multi-layers ANN LMD 384 96 96.94
Proposed method LMD 384 96 99.38

启示

  1. 了解了LMD的具体用法
  2. 基本了解多层脉冲神经网络在故障诊断领域的应用，其实本文是基于作者原来的一篇文章，即脉冲神经网络，本文只是扩展到了多层。
  3. 本文与其他方法对比的时候，仅仅对比了结果，其实训练集，测试集等都不一样，这也是一种避免复现别人论文的方法。